Miten lähteä liikkeelle tehdasfysiikan hyödyntämisessä? Entä voisiko ohjelmistosta olla apua?
Tehdasfysiikan lait ja kaavat ovat ymmärrettäviä sekä todistettuja, mutta usein näiden kaavojen käytäntöönvienti tuntuu yllättävän vaikealta, eikä aina tunnu olevan selvää miten tehdasfysiikan hyödyntämisessä pitäisi lähteä liikkeelle. Tässä artikkelissa käydään läpi yksi mahdollinen malli tehdasfysiikan hyödyntämisessä käytännön toiminnassa.
Tehdasfysiikan kaksi tunnetuinta yhtälöä ovat Littlen laki ja Kingmanin yhtälö.
Littlen laki kertoo jaksoajan, keskeneräisen tuotannon määrän ja läpimenon keskinäisen riippuvuuden:
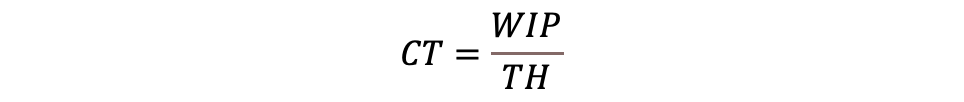
Laajennettu Kingmanin yhtälö (ns. Sakasegawan yhtälö) kertoo kuormitusryhmän eteen muodostuvan jonon keskimääräisen pituuden huomioiden saapumisen vaihtelun, prosessin vaihtelun, käyttösuhteen, työpisteiden lukumäärän ja efektiivisen prosessiajan pituuden:

Kun näitä yhtälöitä tarkastelee, on vaikea tunnistaa suoraan asioita joihin päätöksillä ja kehitystoimenpiteillä voidaan vaikuttaa. Tämän vuoksi on tarpeen purkaa yhtälöitä edelleen muuttujien lähtötasolle, jolloin nähdään selkeämmin pisteet, joita kehittämällä voidaan vaikuttaa prosessiin. Oheiseen taulukkoon on listattu tyypilliset lähtötason muuttujat, joilla pystytään laskemaan Kingmanin yhtälö, Littlen laki sekä lisäksi määrittämään efektiivisen prosessiajan koostumus.
| Lähtöarvot | |
| m | Työpisteiden määrä |
| tw | Työajan määrä aikayksikössä (esim. h/vko) |
| t0 | Yhden yksikön keskimääräinen toteutunut prosessiaika |
| t0nom | Yhden yksikön keskimääräinen nimellinen prosessiaika |
| s0 | Yhden yksikön prosessiajan keskihajonta |
| ta | Yksikköjen keskimääräinen saapumisväli kuormitusryhmälle |
| ts | Keskimääräinen toteutunut asetusaika |
| tsnom | Keskimääräinen nimellinen asetusaika |
| ss | Asetusajan keskihajonta |
| Ns | Keskimääräinen sarjakoko |
| mf | Keskimääräinen häiriön syntymisväli yhdellä työpisteellä |
| mr | Keskimääräinen häiriön korjausaika |
| sr | Korjausajan keskihajonta |
| sa_job | Töiden kuormitusryhmälle saapumisen keskihajonta |
Kaikki taulukon lähtömuuttujat voidaan luonnollisesti määrittää prosessin toteumadatasta esim. Exceliä hyödyntäen. Määrityksessä tulee ymmärtää hyvin eri lähtömuuttujien merkitys ja toimia huolellisesti virheiden välttämiseksi. Kenties suurin virheriski liittyy muuttujien ta ja sa_job -määrityksiin, sillä niissä tulee katsoa kalenteria kuormitusryhmän näkökulmasta (aikaa jolloin kuormitusryhmälle ei ole suunniteltu toimintaa ei myöskään ”ole olemassa”). Tehdasfysiikan käytännön hyödyntämistä helpottamaan on luotu myös CalculateTheProcess -ohjelmisto, joka tekee mm. lähtömuuttujien määrityksen käyttäjän puolesta (calculatetheprocess.com).
Taulukossa olevista lähtömuuttujista voidaan tunnistaa huomattavasti helpommin kohteet, joihin voidaan operatiivisen toiminnan päätöksenteolla ja kehitystoimenpiteillä vaikuttaa. Työpisteiden lukumäärä, työajan määrä aikayksikössä ja sarjakoko ovat asioita, joita voidaan muuttaa päätöksellä. Sen sijaan moniin aikamuuttujiin ja niiden vaihteluun voidaan vaikuttaa erilaisilla kehitystoimenpiteillä. Voidaan esimerkiksi keskittyä pienentämään keskimääräistä asetusaikaa ja/tai asetusajan keskihajontaa.
Oleellista on tunnistaa millaisia päätöksiä ja kehitystoimenpiteitä olisi järkevää tehdä, kun halutaan saavuttaa mahdollisimman hyvä parannus tietyissä prosessin indikaattoreissa. Kuinka sitten lähteä liikkeelle ja päästä hyödyntämään tehdasfysiikkaa? Seuraavaksi kuvataan yksi suositeltava etenemismalli, jolla tehdasfysiikkaa voidaan lähteä viemään käytäntöön.
Suositeltava lähestymistapa
Määrittely
- Rajaus. Aloita rajatusti äläkä tavoittele kaikkea kerralla. Hyvä lähestymistapa on valita esimerkiksi yksi prosessivaihe tarkasteluun.
- Data. Selvitä mitä lähtödataa sinulta löytyy ja tarvitaanko jotain lisää. On tärkeää myös tiedostaa, kuinka luotettavaa data on ja millaisia virhelähteitä datassa mahdollisesti voi olla.
- Mitä kattavammin dataa on käytettävissä, sitä enemmän asioita pystytään analysoinnissa huomioimaan. Hyödyllisiä analyyseja pystytään tyypillisesti kuitenkin tuottamaan jo seuraavilla kolmella eräkohtaisesti prosessista kerätyillä tiedoilla:
i. Eräkoko
ii. Vaiheaika
iii. Erän saapumisaika vaiheen jonoon
- Tarvittaessa voit muuttaa datan keräystapoja. Jo lyhyessä ajassa saadaan usein riittävästi dataa karkeaan laskentaan.
3. Tarkasteltava aikaväli. Päätä tarkasteltava aikaväli ja käytä samaa aikaväliä kaikilla datoilla.
- Oleellista on valita aikaväli, joka kuvaa edustavasti tilannetta jonka haluat laskea. Esim. kesälomakausi ei välttämättä ole soveltuva, ellei juuri sitä haluta tutkia. Tyypillisesti pidempi aikaväli johtaa useampien erikoistilanteiden (lomat, häiriöt, kysynnän muutokset) huomiointiin kuin lyhyt. Tämä ei välttämättä tarkoita että pitkä aikaväli on parempi, vaan tärkeää on ennen kaikkea tiedostaa millaista otantaa aikaväli edustaa.
Mittaus
4. Kerää ja jalosta data kaavoilla laskettavaan muotoon
- Data on hyvä katsoa läpi ja korjata/poistaa mahdolliset virheet
5. Suorita nykytilan laskenta (laajennettu VUT, Littlen laki)
- Visualisoi data ja hyödynnä kuvaajia osoittamaan muuttujien välinen suhde (u, CT, TH sekä WIP ja TH.
- Pilko vaihtelukomponentti V osatekijöihin nähdäksesi paremmin eri vaihtelulähteiden merkittävyyden
Analysointi
- Arvioi tuloksia
- Missä kohtaa VUT-käyrää nykytila on? Onko prosessi stabiili?
- Mikä on jaksoaika ja WIP?
- Mitkä ovat suurimmat vaihtelun lähteet?
- Mitä muuttamalla saavutettaisiin suuri parannus prosessiin?
- Mitä muuttamalla ei saavuteta merkittävää parannusta?
Kehitä
- Valitse potentiaaliset kehityskohteet
- Huomioi vaikuttavuus prosessiin sekä kehitystoimenpiteen vaatimat resurssit ja kustannukset
- Simuloi kehitystoimenpiteitä
- Laske laajennettu VUT ja Little kehitystoimenpiteillä oletettavasti saavutettavilla lähtöarvoilla
- Arvioi simuloinnin tuloksia. Tarvittaessa pohdi kehityskohteita uudelleen ja suorita uusi simulointi.
- Toteuta kehitystoimenpiteet
Tarkasta
- Toiminnan stabiloiduttua laske uusi nykytila ja arvioi toteutuivatko tavoitteet
Pilotointiehdotus ja case-esimerkki: Eräkoon optimointi
Yksi herkullinen kehityskohde on eräkoon (Ns) optimointi jaksoajan (CT) lyhentämiseksi ja KET:n (WIP) pienentämiseksi. Se soveltuu myös hyvin tehdasfysiikan hyödyntämisen pilotointiin, sillä erityisesti teollisuudessa eräkokoa voidaan tyypillisesti muuttaa yksinkertaisella päätöksellä. Toisaalta eräkoolla on monissa tapauksissa myös suuri vaikuttavuus sekä vaihteluun että käyttösuhteeseen, joten optimoinnilla voidaan parhaimmillaan saavuttaa huomattavia tuloksia.
Perinteinen tavoite teollisuudessa on ollut resurssitehokkuuden maksimointi ja näin ollen eräkoko on asetettu varsin suureksi. Lean -ajattelun myötä on monissa yrityksissä alettu tavoittelemaan erityisesti virtaustehokkuutta, jonka vuoksi eräkoko on asetettu kapasiteetin sallimissa rajoissa mahdollisimman pieneksi (mikä on virheellinen tulkinta Leanista eikä johda virtaustehokkuuteen, mutta se on toinen tarina). Kumpikaan ääripää ei kuitenkaan useimmiten tuota kokonaisuuden kannalta hyvää tulosta.
Tässä casessa tarkasteltavaksi on valittu yksi koneistuskeskus, jolla koneistetaan kokoonpanon tarpeisiin erilaisia osia. Tarkastellaan tilannetta, jossa ei esiinny kapasiteettihäviöitä kuten sairaslomia tai konerikkoja. Todellisuudessahan häviöitä jossakin vaiheessa tulee ja ne on myös mahdollista huomioida, mutta oletetaan ne tässä riittävän harvinaisiksi että ne on mielekästä jättää erikseen käsiteltäviksi erikoistilanteiksi. Häiriöt voidaan jättää huomiotta myös mahdollisen datan puutteen vuoksi, kunhan tiedostetaan että laskenta edustaa häiriötöntä tilannetta ja muistetaan huomioida tämä myös johtopäätöksiä tehtäessä.
Aina valmistettavan nimikkeen vaihtuessa tulee koneistuskeskuksellamme tehdä asetus, johon menee keskimäärin 20 minuuttia. Yksi kappale koneistetaan keskimäärin 15 minuutissa. Työt saapuvat keskukselle edeltävästä työvaiheesta päätetyn kokoisina erinä. Tuotannon johto on asettanut keskimääräisen eräkoon 10 kappaleeseen, sillä se on tuntunut riittävän suurelta turhien asetusten välttämiseksi mutta ei kuitenkaan niin suurelta että erän valmistus kestäisi kohtuuttoman kauaa. Näin ollen asetusaika pidentää yhden kappaleen efektiivistä prosessiaikaa keskimäärin 20min / 10 = 2min. Asetukset huomioiva efektiivinen prosessiaika on siis 15min + 2min = 17min.
t0 = 15min
ts = 20min
Ns = 10
ts/Ns = 2min
te = 17min
Kone toimii ilman taukoja kahdessa vuorossa ja sen kapasiteetti näin ollen on 16h/vrk (960min/vrk). Nykyisellä eräkoolla pystyttäisiin siis teoriassa valmistamaan vuorokaudessa 960min / 17min = 56,5kpl. Nykyisellä kuormalla kokoonpano tarvitsee keskimäärin 35 kappaletta vuorokaudessa, joten konetta käytetään 35 / 56,5 = 62 % käyttösuhteella (u).
Tavoitteena on optimoida eräkoko siten, että nykyisellä kuormalla (35kpl/vrk) koneen jaksoaika saadaan mahdollisimman pieneksi. Jos ei huomioida mitään vaihteluelementtejä (saapumisen vaihtelu, koneaikojen vaihtelu, asetusaikojen vaihtelu), on optimaalinen eräkoko helppo laskea. Asetetaan eräkoko sellaiseksi, että koneaikojen ja asetusaikojen summa vastaa koneen kapasiteettia ja näin ollen käyttösuhde nousee 100 %:iin.
(35/Ns)*ts + 35 * t0 = 960min
(35/Ns)*20min + 35 * 15min = 960min
35/Ns = (960min – 525min)/20min
Ns = 1,61
Ilman vaihtelua toimivassa (teoreettisessa) prosessissa olisi siis kannattavaa pudottaa keskimääräinen eräkoko peräti 16 %:iin aiemmasta.
Todellisessa maailmassa em. 100 % käyttösuhde johtaisi tunnetusti rajattomasti kasvavaan keskeneräiseen tuotantoon ja sen myötä rajattomasti kasvavaan jaksoaikaan. Syynä tähän on vaihtelu, jonka seurauksena koneelta aika ajoin loppuu työ ja kapasiteettia menetetään. Koska 100 %:n käyttösuhde edellyttäisi kaiken kapasiteetin hyödyntämistä, johtaa tilanne koneen eteen rajattomasti kertyvään jonoon. Tietysti tuotannon esihenkilö todellisuudessa jonon kasvaessa “pelastaa tilanteen” esimerkiksi teettämällä ylitöitä, mutta tällöin kapasiteetti on todellisuudessa alun perin suunniteltua korkeampi. 100 % käyttösuhde siis toteutuu ainoastaan teoreettisessa tilanteessa.
Vaihtelua syntyy sekä saapumisen vaihtelusta että prosessin vaihtelusta. Esimerkissämme prosessin vaihtelua aiheuttavat asetusajan vaihtelu ja yksikköajan vaihtelu, joihin ei eräkoon muutoksella ole merkittävää vaikutusta. Sen sijaan eräkoko vaikuttaa huomattavasti saapumisen vaihteluun. Asian ymmärtämiseksi kuvitellaanpa vaikka yhden kappaleen tunnissa valmistavaa konetta. Verrataan sitten toisiinsa tilanteita, joissa töitä saapuu koneelle yhden kappaleen erissä tunnin välein ja töitä saapuu tuhannen kappaleen erissä tuhannen tunnin välein. On helppo ymmärtää, että eräkoko aiheuttaa jälkimmäisessä vaihtoehdossa koneelle 0 – 1000 tunnin välillä vaihtelevan jonon, kun taas ensimmäisessä tapauksessa eräkoko ei aiheuta jonoa ollenkaan.
Eräkoon pienentäminen siis pienentää vaihtelua, mikä lyhentää jaksoaikaa. Kääntöpuolena kuitenkin on, että eräkoon pienentäminen lisää asetusten määrää ja näin ollen myös niihin kuluvaa aikaa. Seurauksena on käyttösuhteen nousu, joka pidentää jaksoaikaa. Optimointicasessamme siis tulisi löytää paras mahdollinen kompromissi näiden kahden vaikutuksen väliltä.
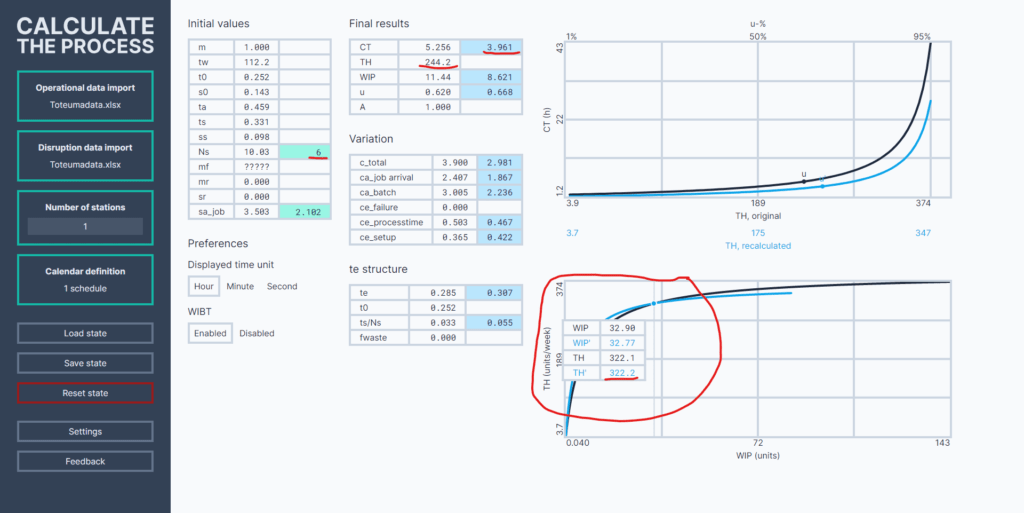
Prosessin ja saapumisen vaihtelukomponentit voidaan määrittää toteumadatasta saatavilla tiedoilla. Datasta määritellyillä lähtömuuttujien arvoilla voidaan edelleen laskea useita tunnuslukuja. Tässä casessa tiedot on määritetty ja jalostettu CalculateTheProcess -ohjelmalla (calculatetheprocess.com). Toteumadatan tiedot on syötetty ohjelmaan Excel -tiedoston kautta.
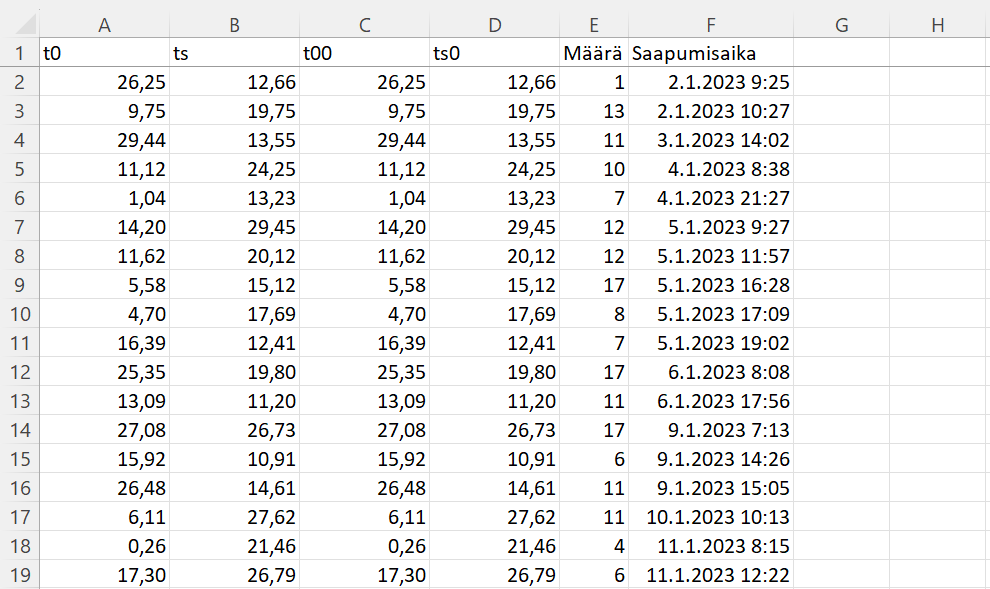
Tuloksena on saatu prosessin nykytilasta mm. seuraavat tiedot:
- Keskimääräinen eräkoko Ns = 10
- Käyttösuhde u = 62 %
- Kokonaisvaihtelu c_total = 3,9
- Jaksoaika CT = 5,26 h

Ohjelmalla simuloimalla havaitaan, että eräkoon pudottaminen arvoon 1 nostaa käyttösuhteen yli 100 %:n eikä siis ole mahdollinen vaihtoehto. Simuloimalla eräkooksi 1,62 tulee käyttösuhteeksi 99,3 %, jolloin jaksoajaksi saataisiin noin 59 h (noin 11-kertainen nykytasoon nähden). Havaitaan siis, että eräkoon asettaminen mahdollisimman pieneksi ei ole kannattavaa. Eräkoolla 2 saadaan jaksoajaksi noin 5,82 h, eräkoolla 3 noin 3,61 h ja eräkoolla 5 noin 3,70 h
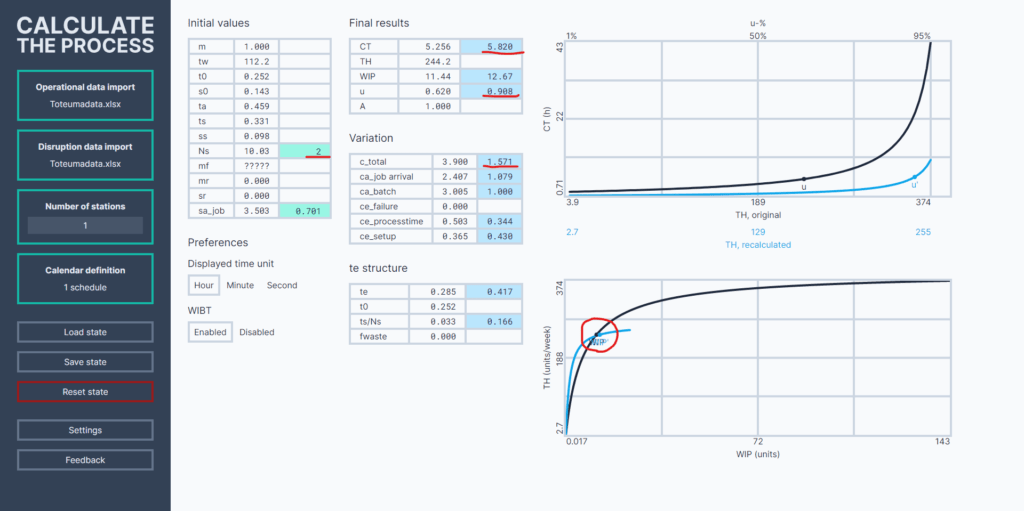
Optimaaliseksi eräkooksi saadaan simuloimalla noin 3,7. Tällöin prosessin tilaksi saadaan seuraavat tiedot:
- Keskimääräinen eräkoko Ns = 3,7
- Käyttösuhde u = 74 %
- Kokonaisvaihtelu c_total = 2,3
- Jaksoaika CT = 3,51 h
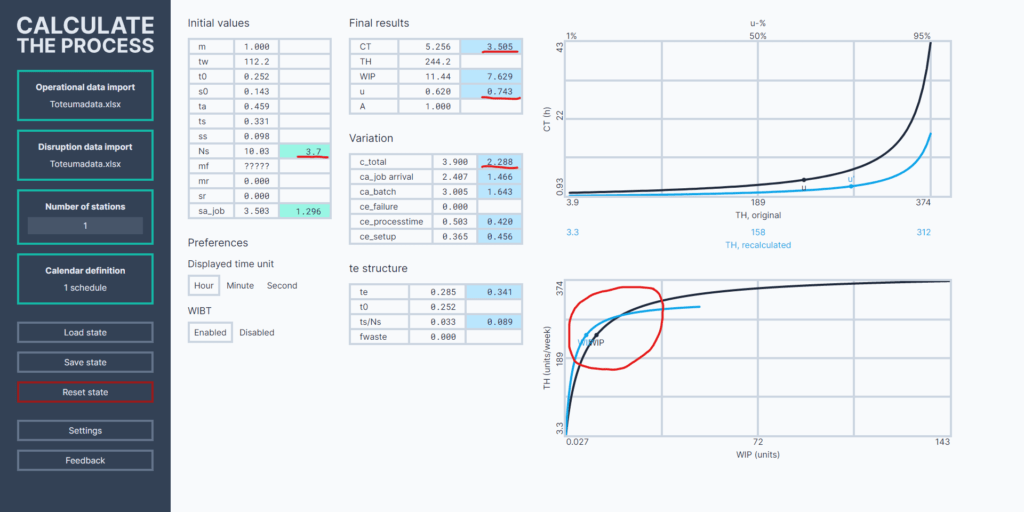
Eräkoon optimoinnilla saataisiin siis lyhennettyä jaksoaikaa 33 % ja pudotettua KET:iin sitoutunutta pääomaa saman verran (kuten Littlen laki meille kertoo). Usein eräkoon muuttaminen voidaan myös tehdä yksinkertaisella päätöksellä ilman rahallista panostusta. Siksi se soveltuu monissa tapauksissa hyvin tehdasfysiikan hyödyntämisen pilotointiin, vaikka luonnollisesti muitakin vaihtoehtoja on lukuisia. Seuraavaksi tulisi viedä kehitystoimenpiteet käytäntöön ja todentaa saadut tulokset myöhemmin toteutettavalla mittauksella.
Herkkyysanalyysi kuorman nousulle
Optimieräkoko muuttuu sitä korkeammaksi, mitä korkeammalla kuormalla tai oikeammin ulostulolla (TH) kuormitusryhmää ajetaan. Tämä voi saada tuotannon esihenkilön pohtimaan, kannattaako casessamme eräkokoa muuttaa nykykuormalla määritettyyn optimiin vaiko varautua mahdollisiin kuormanheilahduksiin pitämällä eräkoko korkeana. Tällainen joko/tai -pohdinta johtaa helposti siihen, että eräkokoa ei muuteta vaan jatketaan kuten ennenkin. Parempi lähestymistapa on jälleen tilanteen analyyttinen arviointi.
WIP – TH -kuvaajassa nykytilakäyrän ja Ns = 3,7 -käyrän leikkauspisteestä voidaan tulkita, että uusi eräkoko 3,7 on vanhaa 10,0:aa parempi niin kauan kuin kuormitus ei nouse yli 20%:a nykyisestä. Jos kuorman nousu nähdään todennäköisenä, ei silti ole kannattavaa vain jatkaa vanhalla ylimitoitetulla eräkoolla. Sen sijaan voidaan hakea soveltuva välimalli nykyisen eräkoon ja nykykuormalla lasketun optimin välillä. Kun eräkooksi asetetaan esimerkiksi 6, saavutetaan jo 25 % pudotus jaksoajassa (sekä KET määrässä) ja eräkoko muuttuu nykyistä kymmentä epäedullisemmaksi vasta kuorman noustua noin 30 % nykytasostaan. Tällöin oltaisiin nykyiselläkin eräkoolla jo siirrytty käyrän epästabiilille alueelle, jolloin toiminta ei enää ole ennustettavaa eikä kyseinen kuormitustaso siis ole järkevä ilman muita vaihtelua vähentäviä kehitystoimenpiteitä. Näin ollen on vaikea keksiä perusteita, joilla nykyinen eräkoko 10 olisi parempi kuin vaikkapa eräkoko 6.
Yhteenveto
Tehdasfysiikan hyödyntämiseen käytännössä voidaan soveltaa edellä esitettyä lähestymistapaa. Tärkeää on rajata tutkittava kohde, kerätä data ja muuttaa laskujen avulla prosessista kerätty mittausdata muuttujiksi, joiden avulla voidaan arvioida erilaisten päätösten ja kehitystoimenpiteden vaikutusta prosessiin. Tällä tavalla operaatioiden problematiikkaa lähestyttäessä päädytään todennäköisemmin laadukkaampiin päätöksiin.
Usein tiedon ja/tai ymmärryksen puute johtaa joko liikaan varovaisuuteen tai vaihtoehtoisesti epäonnistuneisiin kehityshankkeisiin. Siksi on tärkeää, että eri asioiden syy-seurausyhteydet osataan tunnistaa. Useimmiten ääripäät tuottavat erittäin huonoja lopputuloksia ja käytännössä joudutaan valitsemaan kompromissi eri ääripäiden väliltä. Tehdasfysiikka tarjoaa suuria mahdollisuuksia tuon kompromissin optimointiin ja toimenpiteiden vaikutusten simulointiin.
Mikäli CalculateTheProcess -ohjelmisto herätti mielenkiinnon, löydät lisää tietoa sekä yhteystiedot osoitteesta calculatetheprocess.com. Myös Antti Piirainen Quality Knowhow Karjalainen Oy:ltä osaa kertoa asiasta lisää.
Liity postituslistalle
Haluatko samankaltaisia artikkeleita tuoreena suoraan sähköpostiisi? Paina tästä ja liity postituslistalle!
Tilaa artikkelit sähköpostiisiTilaa uutiskirje
Liity postituslistalle ja saat uusimmat artikkelit suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.