Tilastollinen ymmärrys ja käyttö

Tilastollinen ymmärrys ja käyttö 

Lean Six Sigma yhdistettynä Minitab tilasto-ohjelmistoon on tuonut merkittävän tilastoymmärryksen, -osaamisen ja -käytön yritysten suorituskykyjen parantamiseen ja laatuongelmien ratkaisuun. 

Pidän tilastollista ymmärrystä merkittävämpänä ja vaikuttavampana yrityksille kuin itse Lean Six Sigma -projekteja. Projektien tuotoista on Suomessa mustaa valkoisella artikkelissa: Suomalainen Laatu 2020 (1, 2), mutta tilastollisen ymmärryksen, osaamisen ja käytön tuotot/menetykset ovat tuntemattomat. 

Tri W. Edwards Deming varoittaa numeroista ja niihin sokeasti uskomisesta. Hän pitää numerouskoa yhtenä seitsemästä liikkeenjohdon kuolemansynneistä (3): Kaikkein tärkeimpiä numeroita ovat ei tiedossa olevat ja tuntemattomat (”5. Management by use only of visible figures, with little or no consideration of figures, that are unknown and unknowable”).

Olen havainnut, että Lean Six Sigma -koulutus ja joissain kursseissa käytetyt Excel-softat ”liukuvat” kohti tunnettuja numeroita ja erityissyitä. Tämän saman on todennut James L. Bossart artikkelissa ” How the method has evolved—and keeps adapting—over the years” Quality Progress, November 2024. Six Sigma on käynyt läpi viisi kehitysvaihetta viidessä eri ympäristössä sopeutuen uusiin sovellusalueisiin yhä kevyemmillä ja karsituilla laatutyökaluilla – ja alhaisemmilla ambitioilla. Samalla on ohitettu tilastollisen ymmärryksen takana olevat ei tiedossa olevat ja tuntemattomat suorituskykypuutteet. En välttämättä pidä tästä sopeutumisesta – vesittämisestä, mutta kylläkin uusista sovellutusalueista. Lean Six Sigma koulutustaso saattaa laskee ja projektit kohdistua väärin!  Virheet ja reklamaatiot näkyvät. Suorituskykypuutteet ovat näkymättömiä ja tuntemattomia yrityksessä ja vaativat tilastollista ymmärrystä. Viittaan Demingin viiteen kuolemansyntiin. 

Tilastolliset ilmiöt (tuotteet, palvelut ja niiden prosessit) ovat aina läsnä yrityksissä ja tilastollisten menetelmien käyttö on jatkuvaa, kun taas Six Sigma -projekteja tulee silloin tällöin – hyvä niin. Maailma, sen ilmiöt ja luonnonlait tulee nähdä tilastollisina jatkuvasti vaihtelevina tapahtumina – uuden modernin fysiikan näkemys maailmasta. On vaikea kuvitella, että joku voisi tehdä aidon suorituskykyä parantavan Lean Six Sigma -projektin ilman, että ei ymmärrä ja osaa tilastollista ajattelua, konsepteja ja menetelmiä. Näitäkin on nähty, mutta silloin kyseessä on ongelmanratkaisu, erityissyy. Projekti sinänsä saattaa onnistua yksittäisen tuotteen tai syyn osalta, mutta päteekö ratkaisu nyt ja tulevaisuudessa koko yritykseen ja sen kaikkiin tuotteisiin, suorituskykyyn. Epäilen. Tehotonta ja kallista Lean Six Sigman käyttöä! Parempi olisi käyttää jotain ongelmanratkaisumenetelmää kuten juurisyyanalyysia RCA, 8D, A3 jne.   

Työkalut ja työkalusoftat eivät riitä! Lean Six Sigma on vain pieni osajoukko tilastokonsepteista ja menetelmistä. Jotta hallitset koko alueen, tarvitset tueksesi laajan tilastokoulutuksen mielellään Lean Six Sigma -kurssin yhteydessä tai sitten erikseen ja tietysti hyvän ja ”täysverisen” softan. 

Lean Six Sigma -projekti antaa hyvän ja konkreettisen pohjan kaikkien tilastollisten menetelmien oppimiseen, jos kurssi on näin rakennettu (sisältää laajan tilasto-paketin) Six Sigman alkuperäisten konseptien mukaisesti (Mikel Harry: Six Sigma (4)).

Seuraavassa lyhyt kertaus ja katsaus keskeisiin tilastollisiin käsitteisiin, jos ne ovat jostain syystä hämärtyneet tai unohtuneet.

Sisältö:

1. Johdanto
2. Kuvioiden (patterns) paljastaminen kuvaavien tilastojen avulla
3. Ennusteiden tekeminen päättelytilastojen avulla
4. Populaatio
5. Näytteenotto
6. Kaltaistus
7. Tilastolliset menetelmät
8. Ryhmien välisten erojen analysointi
9. Muuttujien välisten suhteiden analysointi
10. Kokeet
11. Täydentävät laatutekniikan työkalut
12. Tilastolliset väärinkäytökset
13. Yhteenveto

1. Johdanto

Tilastot ovat joukko työkaluja, joita käytetään tietojen järjestämiseen ja analysointiin ja ennustamiseen. Tietojen on oltava joko numeerista alkuperää tai tutkijoiden numeroiksi muuntamia arviointeja. Ei ole asiaa, jota ei voisi numeroiksi muuttaa!

Useat henkilöt valittavat, että eihän meidän yrityksessä ole numeroita, joita voisi tilastollisesti käsitellä, saati käyttää SPC:tä. Kyllä on! Katso uutta kirjaamme Laatutaulu – Tehokas menetelmä laadunohjaukseen ja paranukseen, 2024 (5). Olemme esittäneet kirjassa, kuinka asiat/prosessit ja niissä olevat poikkeamat ja virheet voidaan luokitella ja määrittää ja löytää luokille esiintymistiheys tunneittain, päivittäin, viikoittain. Esiintymistiheys on se tilastollinen data, jota voidaan käyttää tilastolliseen laadunohjaukseen (SPC) ja parannukseen mittausdatan lisäksi.  Et tarvitse satoja datoja 2-3 kpl/jakso riittää. Tulokset puhuvat puolestaan. Esitetty kirjassamme.

Laatutaulu – Tehokas menetelmä laadun ohjaukseen ja parantamiseen

47,00 € + alv (10%)

Kaiken voi arvioida ja muuttaa numeroiksi – jopa tanssin (vrt. Tanssii tähtien kanssa). Näiden numeroiden avulla voidaan analysoida ei vain yhtä tanssiliikettä vaan koko tanssia (= populaatio). Samoin voidaan tehdä esimerkiksi tuotteiden pintojen laadulle tai vaikkapa asiakkaiden palvelukokemukselle käyttämällä erilaisia asteikoita. Kohteita on lukemattomia. Tunnetuin asteikko on ns. Likert-asteikko 0-5. 

Yrityksen on päätettävä, mitkä asiat mitataan ja mitkä saatetaan numeroiden muotoon ja tilastollisen analyysin alle kokonaistarkastelua varten!

Liikkeenjohdolle statistiikka ja numerot ovat kaikki kaikessa. Statistiikka on datan tiede. Hyvä opas liikkeenjohdon tilastolliseen analysointiin on D. Wheelerin kirja: Understanding Variation – The Key to Managing Chaos (6). Kirjassa Don esittelee keskeisten liikkeenjohdon avainmittareiden analysointia tilastollisesti aikasarjoina. Toinen peruskirja voisi olla D. Moore ect: The Practice of Business Statistics – Using Data for Desissions (7), jossa esitellään laajemmin datatiedettä. 

Tilastojen takana on siis tilastolliset menetelmät ja menetelmien takana tilastollinen ymmärrys, joiden avulla reaalimaailman ilmiöitä kuvaavat numeeriset tai kvantitatiiviset (määrälliset) poikkeamatiedot jalostetaan sellaiseen muotoon, että ilmiöitä koskevat johtopäätökset on mahdollista tehdä suuremmasta joukosta. Tätä joukkoa kutsutaan vanhahtavalla nimellä populaatioksi. (Tilastotekniikka kehittyi ihmispopulaation ominaisuuksien analysoinnista!)  Tiedot tiivistetään graafisiksi esityksiksi, tunnusluvuiksi ja tietoja tuottavien prosessien tilastollisiksi malleiksi (esim. DoE, Taguchi, Shainin) – ja Sinun ymmärryksesi yrityksestä ja sen käyttäytymisestä kasvaa valtavasti ja voit tehdä merkittäviä päätöksiä kaikista yrityksen tuotteista ja palveluista – jo tehdyistä ja tulevista.  

Tilastojen käyttö palvelee kahta tarkoitusta, 1) kuvausta ja 2) ennustamista: 

Kuvaus: Tilastoja käytetään kuvaamaan vaikuttavien tekijöiden (x) ja ryhmien ominaisuuksia Y. Yhdellä tuotteella tai palvelulla saattaa olla ominaisuuksia muutamasta kymmeniin. Näille ominaisuuksille on määritetty haluttu arvo, arvoväli, luonnehdinta (speksi) jne. Näitä ominaisuuksia aikaansaa lukuisat muuttujat yhdessä ja erikseen (x, tekijä, faktori, parametri jne). Tieto ominaisuuksien ja tekijöiden välisistä suhteista Y≈f(x) on avain onnistumiseen ja tuottavuuteen. 

Tiedot kerätään ja tallennetaan jokaisesta tärkeästä tutkittavasta tai seurattavasta ominaisuudesta ja siihen mahdollisesti liittyvistä muuttujista. Kuvaavia tilastoja voidaan sitten käyttää paljastamaan kunkin muuttujan tietojen jakautuminen/ jakauma, niiden yhteys (korrelaatio) ominaisuuteen ja mahdollisiin muihin tekijöihin ja ulostuloihin. Kun yhteydet löydetään, avautuu mahdollisuus tutkia vaikutusta, kausaliteettia ja edelleen löytää tie parannukseen. Analyysiä voi tehdä niin jatkuville (variabel/continuous) kuin luokitelluille (discret/categorial) muuttujille ja muuttujilla.

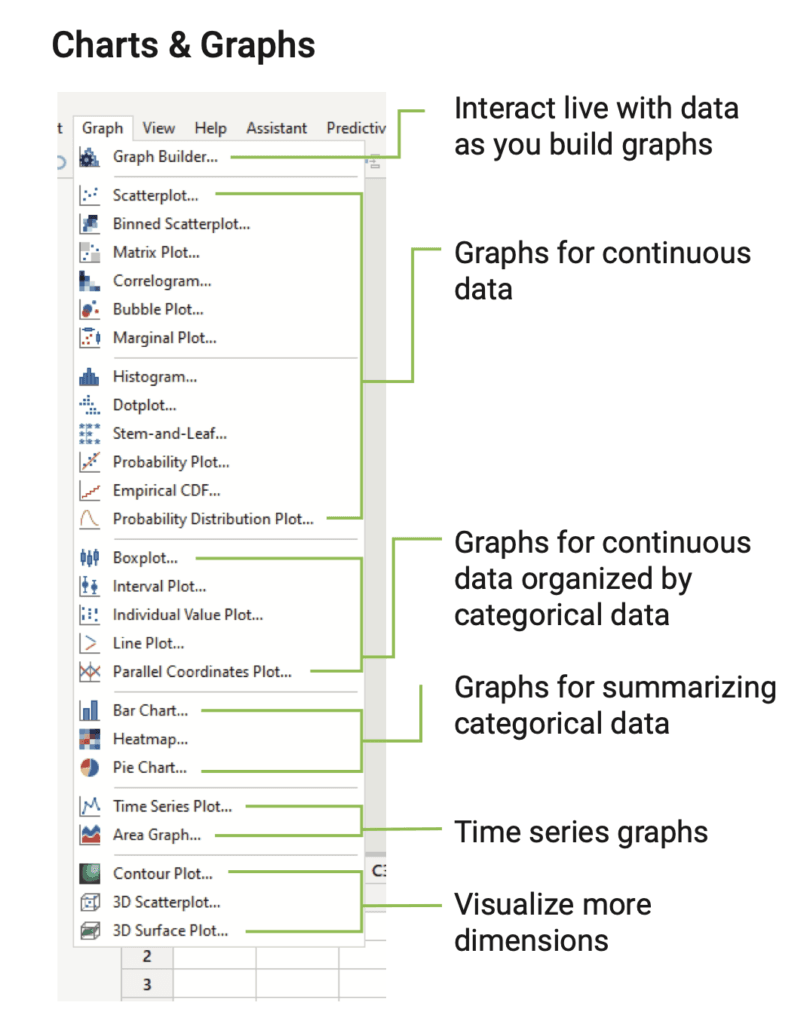
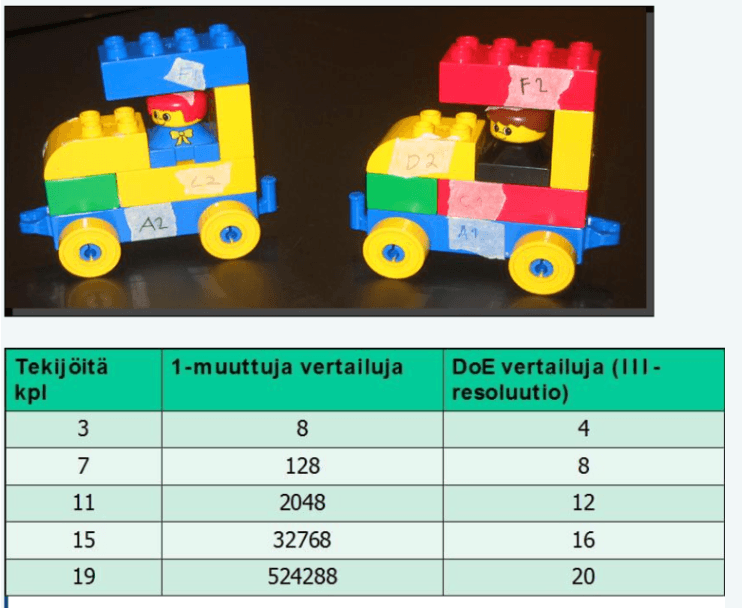
Ennustaminen: Tilastoja käytetään usein myös ennustamiseen. Ennustaminen perustuu yleistettävyyden käsitteeseen: jos tietystä tuotteesta, palvelusta tai niiden syntyprosessista kerätään riittävästi tietoa tietyllä tavalla (Predictive Analytics, DOE, latinalainen neliö, ortogonaalinen matriisi jne.), niin prosessista kerätyn tiedon analysoinnissa paljastetut mallit voidaan yleistää (tai ennustaa). Vaadittava datamäärä ei ole valtava, 4 – 20 kpl (12). Kehittyneimmät ohjelmat optimoivat halutun ulostulon perusteella sisäänmenomuuttujat (Minitab Optimizer). Annat halutun ominaisuuden arvon Y, ja ohjelma ennustaa, millä sisäänmenojen x₁…x_n yhdistelmällä kyseinen ulostulo syntyy!  Voit myös maksimoida tai minimoida. Aivan hämmästyttävä monimuuttujaoptimointi! Artikkelissani Prosessin ja työkoneen säätäminen ja asettaminen – OSA IV on tarkemmin selvitetty Derringerin luomaa menetelmää (8).

Kyky ennustaa on pohja parantamiselle. Demingin PDSA -ympyrä on ennustamisen ympyrä (jatkuvan parantamisen ympyrä). Ennuste siitä, mitä tapahtuu vastaavassa tilanteessa, on todennäköisyys. Tutkija ei ole varma, että samat asiat tapahtuvat muissa yhteyksissä; sen sijaan tutkija voi vain kohtuudella odottaa, että samat asiat tapahtuvat. Tämä on tätä uutta fysiikan ja laadun tulkintaa! Ennustemalleja luotaessa vaaditaan usein tiedoilta/datalta erityisiä ominaisuuksia – riippumattomuutta, edustavuutta, tasapuolisuutta jne.

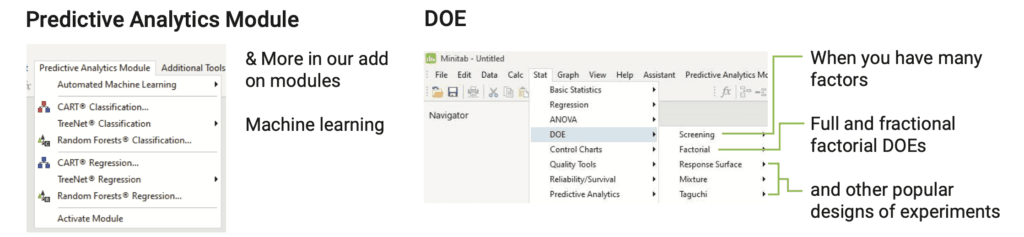
Satunnaisilmiö: Reaalimaailman ilmiöt (tuotteet, palvelut) ovat aina tilastollisia satunnaisilmiöitä, jos seuraavat ehdot toteutuvat:

1. Ilmiöllä on useita erilaisia ulostulovaihtoehtoja, vaihtelua
2. Sattuma määrää, mikä vaihtoehto ulostulosta tulee
3. Vaikka ilmiön ulostulo vaihtelee toistettaessa satunnaisesti, ilmiön tulosvaihtoehtojen osuuksien jakauma käyttäytyy ilmiön toistuessa tilastollisesti stabiilisti.

Isaac Newtonin vuonna 1687 luoma eksakti maailma on kuollut! Eläköön uusi Albert Einsteinin tilastollinen suhteellisuusteoriaan (1915) ja Werner Heisenbergin kvanttimekaniikkaan (1925) perustuva todennäköisyyksien ja tilastollisuuden maailma.

”Newtonin fysiikan puitteissa voimme ennustaa tulevaisuuden täsmällisesti, jos vain tiedämme tarpeeksi lähtötilanteesta ja osaamme laskea. Kvanttimekaniikassa voimme vain laskea todennäköisyyksiä”. (9) Kvanttifysiikka kvanttitietokoneineen on tätä ja huomista päivää, modernia fysiikkaa.

Tri Walter Shewhart toi uuden todennäköisyyksiin ja tilastollisuuteen perustuvan modernin fysiikan laatukenttään 1931 (10) – laatuteoria, erityissyy ja satunnaissyyt (assignable cause, common causes). 

Tilastollinen stabiilisuus on avainsana (käytetään myös sanaa ohjattavuus, controlled), jolla ilmaistaan, että datassa ei ole erityissyitä (special cause). Jos erityissyitä on, malli ei toimi. Tulosvaihtoehdot ovat mitä sattuu! Tilastollisen stabiiliuden/ohjattavuuden saavuttaminen on kaikkein tärkeintä yritykselle. Voiko työn tulos olla mitä sattuu? Ei voi! Tuotteet ja palvelut on ennalta suunniteltuja.

Walter A. Shewhart määritteli ohjattavuuden seuraavasti: ”Ilmiön sanotaan olevan ohjauksessa, kun menneen kokemuksen perusteella voimme kuvata ainakin rajat, kuinka prosessi tulee käyttäytymään tulevaisuudessa.” (A phenomenon will be said to be controlled when, though the use of past experience, we can predict, at least within limits, how the phenomenon will wary in the future. (8) Rajat Shewhart määritteli kokemuspohjalta ±3 sigmaksi (SPC-rajat). 

Luonnollisen satunnaisilmiödatan perusteella ei kuitenkaan voi muodostaa numeerista mallia, vaikka näin moni uskoo. Input(tien) datan (x) on oltava hallittu, ei satunnainen, jotta malli voidaan luoda oikein ja mallin tulokset ovat tilastollisesti stabiilit. 

Säätietoja kerätään valtavasti eri paikkakunnilta. Perustuuko sään ennustaminen näihin tietoihin. Ilmatieteenlaitoksen sivut toteavat: ”Numeerinen säänennustusjärjestelmä on monimutkainen tietotekninen sovellus, joka koostuu useista osista. Itse sääennustusmalli kykenee jäljittelemään eli simuloimaan ilmakehän prosesseja ja ilmiöitä fysiikan lakeihin perustuen. Se ei siis ole tilastollinen malli, jossa havaintoihin ja aiemmin toteutuneisiin sään kehityskulkuihin perustuen arvioitaisiin sään tulevaa kehitystä, vaan malli pyrkii toimimaan mahdollisimman tarkkaan oikean ilmakehän mukaisesti.”https://www.ilmatieteenlaitos.fi/saanennustusmallit (11) 

Mallin rakentamiseksi tarvitaan oikeanlainen näytteenotto (sampling). Näytteenottomallit (matriisit) löytyvät hyvistä softista DoE:n valikon alta. Kuva 2. Katso myös artikkeli Seulontakokeiden tehokas käyttö (12).

Todennäköisyyslaskenta: Jotain tärkeää vielä puuttuu kokonaisuudesta. Todennäköisyyslaskennan (teoreettinen) tehtävänä on tuottaa matemaattisia malleja prosesseille, jotka generoivat reaalimaailman ilmiöitä kuvaavia numeerisia tai kvantitatiivisia datoja, joihin liittyy epävarmuutta ja satunnaisuutta. Minitabissa malleja on Chi-Square -jakaumasta Weibull-jakaumaan. Näitä malleja sanotaan usein tilastollisiksi malleiksi, stokastisiksi malleiksi tai todennäköisyysmalleiksi. Soveltava tilasto-/datatiede, esimerkiksi laatutekniikka, soveltaa teoreettisen tilastotieteen kehittämiä malleja reaalimaailman ilmiöihin. Andrew Sleeper esittelee kirjassa Six Sigma Distribution Modeling (13) keskeiset tilastolliset mallit ja niiden sovellutuskentän kuin myös Matthew Barsalow Applied Statistics Manual (14) kirjassaan.

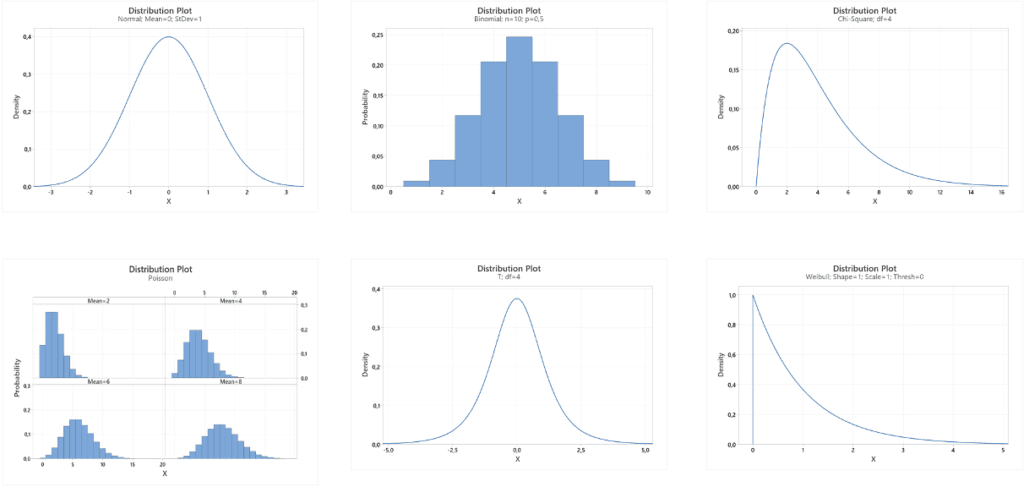
2. Kuvioiden (pattern) paljastaminen kuvaavien tilastojen avulla

Kuvaavat tilastot ”kuvailevat” kerättyä satunnaista tietoa/dataa. Yleisesti käytettyjä kuvaavia tilastoja ovat taajuusluvut, vaihteluvälit (korkeat ja alhaiset pisteet tai arvot), keskiarvot, moodit, mediaanipisteet ja keskihajonnat. Nämä ovat samalla mahdollisen mallin parametreja, joilla reaalimaailmaa sovitetaan malliin. 

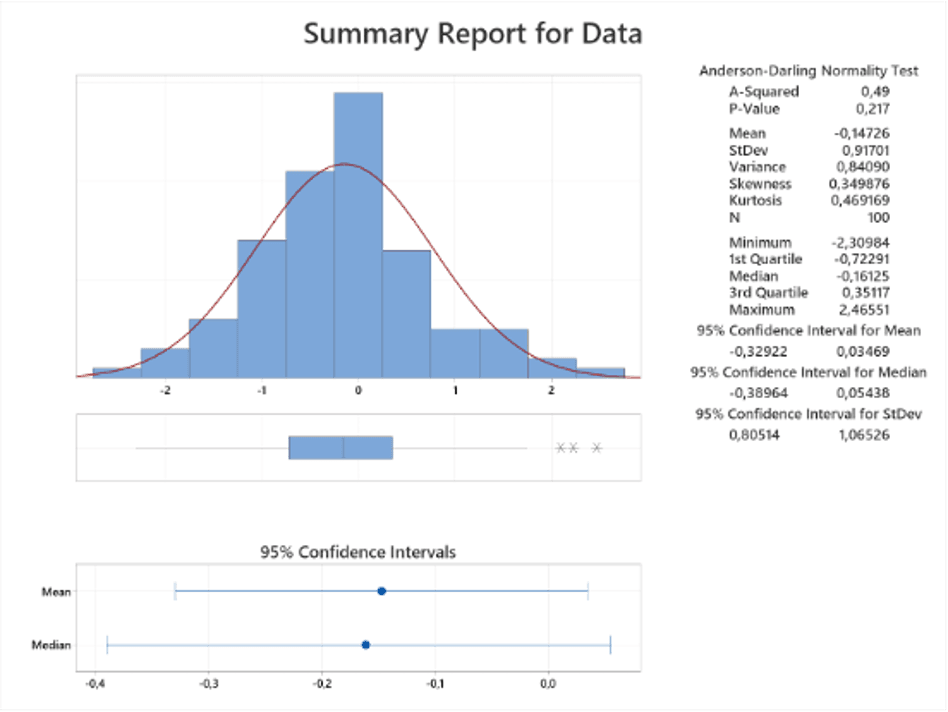
Kaksi käsitettä ovat välttämättömiä kuvaavien tilastojen ymmärtämiseksi: muuttujat ja jakaumat.

2.1. Muuttujat 

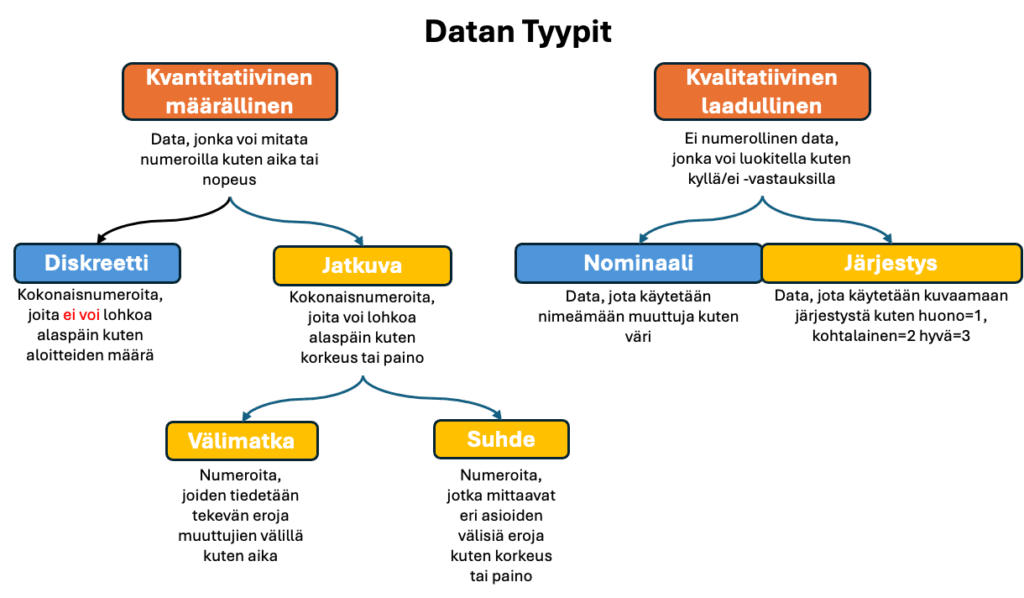
Tilastoja käytetään numeerisen datan tutkimiseen. Numeeriset tiedot ovat havaintoja, jotka tallennetaan numeroiden muodossa. Luvut ovat luonteeltaan vaihtelevia, mikä tarkoittaa, että määrät vaihtelevat tiettyjen tekijöiden mukaan. Esimerkiksi, kun analysoidaan tuotteiden vaihtelua, löydetään usein lämpötilan, paineen, työstönopeuden ja terän aiheuttamaa vaihtelua. Sama on asianlaita palveluiden osalta. Tilastoissa näitä syitä kutsutaan muuttujiksi. Muuttujat on jaettu joko kahteen, kolmeen tai neljään perusluokkaan, riippuen siitä kuka ja kuinka niitä käytetään.

2.1.1. Nominaalimuuttujat (nominaali, diskreetti, attribuutti, lukumäärä)

Nominaalimuuttujat luokittelevat tiedot arvoluokkiin. Tämä prosessi sisältää luokkien merkitsemisen ja sitten esiintymistiheyden laskemisen. Tutkija saattaa haluta vertailla kokeiden arvosanoja mies- ja naisopiskelijoiden välillä. Taulukot koottaisiin käyttämällä luokkia ”mies” ja ”nainen”. Sukupuoli olisi nominaalimuuttuja. Huomaa, että itse luokat eivät ole kvantitatiivisia, määrällisiä. Mies- tai naispuolisuus eivät ole luonteeltaan numeerisia, vaan kunkin luokan esiintymistiheydet johtavat kvantitatiivisiin tietoihin – 12 miestä ja 9 naista.

2.1.2. Ordinaalimuuttujat (ordinaali, kuokittelu, attribuutti, lukumäärä)

Järjestysmuuttujat järjestävät (tai ”rankkaavat”) tiedot asteittain. Järjestysmuuttujat eivät määritä numeerista eroa datapisteiden välillä. Ne osoittavat vain, että yksi datapiste on korkeammalla tai alempana kuin toinen. Tutkija saattaa esimerkiksi haluta analysoida oppilaiden kokeissa annetut kirjainarvosanat. A olisi korkeampi kuin B ja B korkeampi kuin C. Näiden datapisteiden välistä eroa, A:n ja B:n tarkkaa etäisyyttä ei kuitenkaan ole määritelty. Kirjainarvosanat ovat esimerkki järjestysmuuttujasta, jotka voidaan edelleen muuntaa numeroiksi 1, 2 ja 3.

2.1.3. Intervallimuuttujat (intervalli, jatkuva, variaabeli, mittaustulos)

Silloin, kun tietojen järjestys tunnetaan samoin kuin tarkka numeerinen etäisyys datapisteiden välillä tunnetaan, on kyse intervallimuuttujasta. Tutkija voi analysoida kokeiden todelliset prosenttipisteet olettaen, että opettaja antaa prosenttipisteet. Pistemäärä 88 (A) on korkeampi kuin pistemäärä 76 (B), mikä on korkeampi kuin pistemäärä 72 (C). Näiden kolmen datapisteen järjestys ei ole tiedossa, vaan myös tarkka etäisyys niiden välillä on 12 prosenttiyksikköä kahden ensimmäisen välillä, 4 prosenttiyksikköä kahden toisen välillä ja 16 prosenttiyksikköä ensimmäisen ja viimeisen datapisteen välillä. 

2.1.4. Suhdeasteikko (suhde, jatkuva, variaabeli, mittaustulos)

Suhdeasteikko on yleisin ja kaikkein käyttökelpoisin. Asteikossa on todellinen nollapiste ja myös negatiiviset arvot ovat mahdollisia.  Mitataan jatkuvia, numeerisia muuttujia. 

2.2. Jakaumat

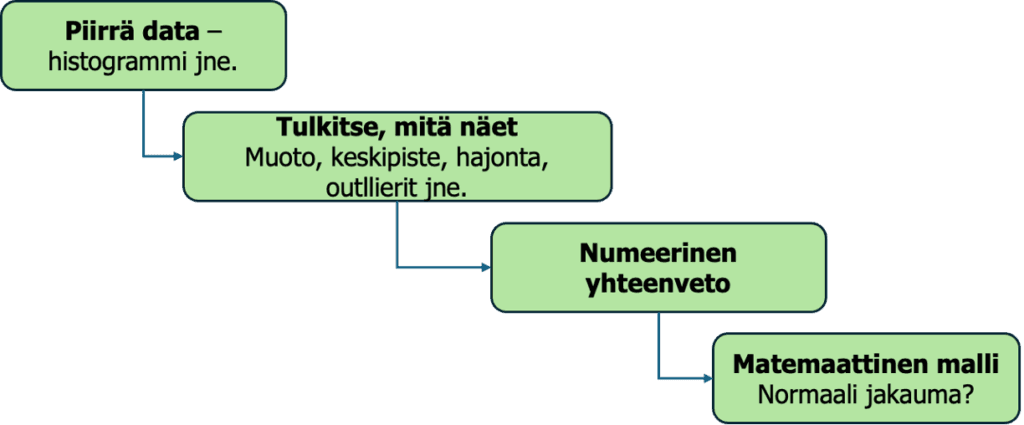
Jakauma on datan graafinen esitys. Datapisteiden yhdistämisestä muodostuvaa viivaa kutsutaan taajuusjakaumaksi. Tämä viiva voi olla monimuotoinen. Tärkein yksittäinen muoto on kellon muotoinen käyrä, joka luonnehtii jakautumista ”normaaliksi”. Täysin normaalijakauma on vain teoreettinen ihanne. Tämä ihanne on kuitenkin olennainen ainesosa tilastollisessa päätöksenteossa. Jotta tämä toimii, on tilastollisia ohjeita noudatettava (esim. satunnainen näytteenotto). Täysin normaalijakauma on matemaattinen rakennelma, joka kantaa mukanaan tiettyjä matemaattisia ominaisuuksia, jotka auttavat kuvaamaan jakauman attribuutteja. Vaikka todellisiin datapisteisiin perustuva taajuusjakauma harvoin, jos koskaan, täysin vastaa täysin normaalia jakaumaa, taajuusjakauma voi usein lähestyä tällaista normaalia käyrää.

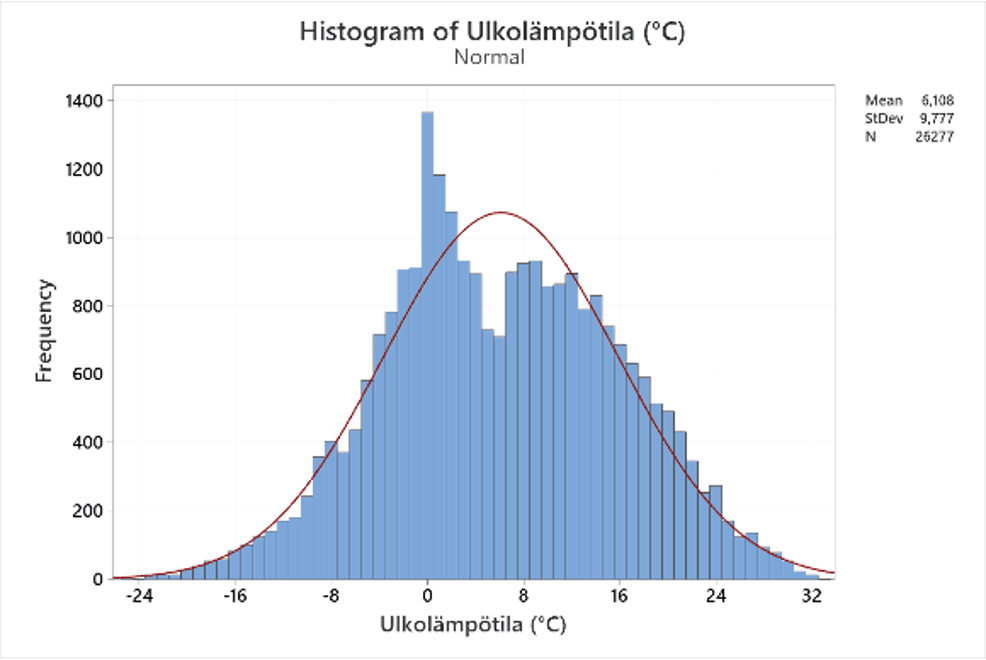
Mitä lähempänä taajuusjakauma muistuttaa normaalikäyrää, sitä todennäköisemmin jakauma säilyttää samat matemaattiset ominaisuudet kuin normaalikäyrä. Tämä on tärkeä tekijä kuvattaessa taajuusjakauman ominaisuuksia. Kun taajuusjakauma lähestyy normaalia käyrää, voidaan tehdä varmemmin yleistyksiä siitä tietojoukosta, josta jakauma on johdettu. Ja juuri tälle yleistettävyyden käsitteelle tilastot perustuvat. On tärkeää muistaa, että kaikki taajuusjakaumat eivät lähennä normaalia käyrää. Jotkut ovat vinossa, dataa voi puuttua kuten kuvassa jne. Kun taajuusjakauma on vinossa, normaalikäyrälle ominaiset ominaisuudet eivät enää päde. Joissain tapauksissa jakauman voi muuntaa normaaliseksi. Katso artikkeli: Suorituskykyanalyysit ei-normaalille datalle (15).

Tilasto-ohjelmalla voit hakea/sovittaa parhaiten dataasi sopivaan tilastojakaumaan.

3. Ennusteiden tekeminen päättelytilastojen avulla

Päättelytilastoilla tehdään johtopäätöksiä ja ennusteita tietojen kuvausten perusteella. Kirjoituksessa käytetyt keskeiset käsitteet ovat todennäköisyys, populaatiot ja otanta.

3.1. Kokeet (experiments)

Tyypillisessä kokeellisessa tutkimuksessa kerätään tietoa kahden tai useamman ryhmän käyttäytymisestä, asenteista tai toimista ja yritetään vastata tutkimuskysymykseen (kutsutaan usein hypoteesiksi). Aineiston analyysin perusteella tutkija voi sitten yrittää kehittää kausaalimallin, joka voidaan yleistää populaatioihin.

Kysymys, jota voitaisiin käsitellä kokeellisella tutkimuksella, voisi olla ”Tuottaako lämpötilan prosessimuutos paremman saannon tai parempia tuotteita?” ”Tuottaako palvelun muutos (x) lyhyemmän läpimenoajan ja paremman hoitotuloksen?” Koska olisi mahdotonta ja epäkäytännöllistä tarkkailla ja tutkia kaikki prosessin tuottamat tuotteet tai palvelut, tutkija tutkii otosta – tai osajoukkoa – populaatiosta.  

Näytteenottoa (sampling) – tai tämän populaation osajoukon luomista – käyttävät monet tutkijat, jotka haluavat ymmärtää jotakin ilmiötä. Näytteenottotapoja on lukuisia esim. yksimuuttujakokeessa, 2t testi ja monimuuttujakokeissa ortogonaalimatriisi. Katso artikkeli: Muutanko yhtä tekijää vai useita tekijöitä? OFAT vai DoE? (16).

3.1.1 Riippuvat muuttujat (dependent variables)

Kokeellisessa tutkimuksessa muuttujaa, jonka tulos riippuu toisesta muuttujasta (tai määräytyy tai johtuu toisesta muuttujasta), kutsutaan riippuvaksi muuttujaksi Y. Kokeessa voidaan esimerkiksi selvittää, missä määrin tuotteen tai palvelun laatuun vaikuttaa se, miten paljon prosessissa tehdään virheitä. Tässä tapauksessa riippuva muuttuja olisi tuotteen tai palvelun laatu.

3.1.2. Riippumattomat muuttujat (independent variables)

Kokeellisessa tutkimuksessa muuttujaa, joka määrittää (tai aiheuttaa) riippuvan muuttujan tuloksen, kutsutaan riippumattomaksi muuttujaksi (x). Kokeessa voidaan esimerkiksi selvittää, missä määrin prosessin aikana tehty prosessimuutos/parannus vaikuttaa lopputulokseen. Tässä tapauksessa riippumaton muuttuja olisi se, millainen prosessimuutos on.

3.2. Todennäköisyys

Aloittelevat tutkijat käyttävät useimmiten sanaa todennäköisyys ilmaisemaan subjektiivista arviota tietyn tapahtuman todennäköisyydestä tai varmuusasteesta. Ihmiset sanovat sellaisia ​​asioita kuin: ”Huomenna sataa lunta luultavasti.” ”On epätodennäköistä, että voimme voittaa pallopelin.” Ennustettavalle tapahtumalle on mahdollista antaa numero, 0 ja 1 välillä, mikä edustaa tapahtuman toteutumisen varmuutta. Opiskelija saattaa esimerkiksi sanoa, että todennäköisyys, että ohjaaja antaa arvion kokeesta ensi viikolla, on noin 90 prosenttia tai 0,9. Kun 100 prosenttia eli 1,00 edustaa varmuutta, 0,9 tarkoittaisi, että opiskelija on melkein varma, että opettaja antaa kokeen. Jos opiskelija antaisi numeron 6, kokeen todennäköisyys olisi vain hieman suurempi kuin todennäköisyys, että tenttiä ei tehdä. Arvosana 0 osoittaisi täydellistä varmuutta siitä, ettei koetta anneta.

Tietyn tuloksen tai tulosjoukon todennäköisyyttä kutsutaan p-arvoksi. Keskustelussamme p-arvoa symboloi p-kirjain, jota seuraa sulkeet, jotka sisältävät tuloksen tai tulosjoukon symbolin. Esimerkiksi p(X) tulisi lukea ”tiedon X-pistemäärän todennäköisyys”. Siten p(tentti) tulee lukea ”todennäköisyys, että ohjaaja palauttaa kokeen ensi viikolla.” 

Lue artikkeli: Tulkitse p:tä – mitä tilastollisilla menetelmillä on tekemistä todellisuuden kanssa? (17)

4. Populaatio

Populaatio on ryhmä, jota tutkitaan. Tuotannossa populaatio on kaikki tiettyä tuotetta olevat yksilöt ja palvelussa kaikki palvellut henkilöt. Tutkijat pystyvät harvoin tutkimaan jokaista populaation jäsentä. Yleensä he tutkivat sen sijaan edustavaa otosta – tai osajoukkoa – populaatiosta. Tämän jälkeen tutkijat yleistävät otosta koskevat havainnot koko populaatiolle. Populaatio nimi on vanhahtava nimi koko joukosta, kuten aikaisemmin on mainittu.

5. Näytteenotto

Näytteenotto suoritetaan niin, että tutkittava populaatio voidaan pienentää hallittavaan kokoon. Tämä voidaan saavuttaa satunnaisotannalla, jota käsitellään seuraavaksi. 

Satunnaisotos on tutkijoiden käyttämä menetelmä, jossa kaikilla tietyn kokoisilla näytteillä on yhtäläinen mahdollisuus tulla valituksi havainnointiin, kokeeseen jne. Otokseen valituista jäsenistä ei ole ennalta määrättyä. Tämäntyyppinen näytteenotto tehdään satunnaisotoksena harhojen minimoimiseksi ja tarjoaa suurimman todennäköisyyden, että näyte todella edustaa suurempaa populaatiota. Tarkoituksena on tehdä otoksesta mahdollisimman edustava populaatiosta. Yleensä otoksen suuruus voidaan laskea tiettyjen parametrien vallitessa. Hyvät ohjelmistot antavat arvion siitä, kuinka pieni tai suuri näytteen on oltava ja kuinka se on otettava. Huomaa, että mitä lähempänä otosjakauma on likimääräistä populaatiojakaumaa, sitä yleisempiä ovat otantatutkimuksen tulokset populaatiolle. Tässä pätevät todennäköisyyskäsitteet. Satunnaisotanta tarjoaa suurimman todennäköisyyden, että datajakauma otoksessa on läheisesti likimääräinen datan jakautuminen populaatiossa.

6. Kaltaistus (Matching)

Kaltaistus on menetelmä, jota tutkijat käyttävät saadakseen tarkkoja ja täsmällisiä tuloksia tutkimuksesta, jotta niitä voidaan soveltaa suurempaan populaatioon. Kun populaatio on tutkittu ja otos valittu, tutkijan tulee ottaa huomioon muuttujat tai ulkoiset tekijät, jotka voivat vaikuttaa tutkimukseen. Kaltaistusmenetelmiä sovelletaan, kun tutkijat ovat tietoisia ulkoisista muuttujista ennen tutkimuksen suorittamista. Ryhmien yhdistämiseen käytetään kahta menetelmää:

6.1. Tarkkuuskaltaistus

Tarkkuuskaltaistuksessa on kokeellinen ryhmä, joka sovitetaan vertailuryhmään. Molemmilla ryhmillä on pohjimmiltaan samat ominaisuudet. Siten ehdotettu tutkittava syy-suhde/malli mahdollistaa todennäköisyyspohjaisen oletuksen, että tulos on yleistettävissä.

6.2. Taajuusjakauma

Taajuusjakauma on hallittavampaa ja tehokkaampaa kuin tarkkuuskaltaistus. Yksi-yhteen sovituksen sijaan, joka on annettava tarkkuuskaltaistuksessa, frekvenssijakauma mahdollistaa koe- ja kontrolliryhmän vertailun asiaankuuluvien muuttujien kautta. Esimerkiksi miehiä ja naisia on yhtä paljon. 

Vaikka teoriassa vastaavuudella on taipumus tuottaa päteviä johtopäätöksiä, syntyy melko ilmeinen vaikeus löytää aiheita, jotka ovat yhteensopivia. Tutkijat saattavat jopa uskoa, että koe- ja kontrolliryhmät ovat identtisiä, vaikka itse asiassa monet muuttujat on jätetty huomiotta. Näistä syistä tutkijoilla on taipumus hylätä täsmäytysmenetelmät satunnaisen otannan hyväksi.

7. Tilastolliset menetelmät

Tilastojen avulla voidaan analysoida yksittäisiä muuttujia, muuttujien välisiä suhteita ja ryhmien välisiä eroja. Tilastojen avulla voidaan analysoida yksittäisiä muuttujia, muuttujien välisiä suhteita ja ryhmien välisiä eroja.

7.1. Yksittäisten muuttujien analysointi

Yksittäisen ryhmää kuvaavan muuttujan (kuten populaation tai edustavan otoksen) analysointiin käytetyt tilastolliset menetelmät sisältävät keskeistendenssisyyden (so. missä on ”keskusta”) ja vaihtelun mittareita. Tutkiakseen näitä mittareita tutkijan on ensin otettava huomioon tietyn muuttujan jakauma tai arvoalue populaatiossa tai otoksessa. Normaalijakauma tapahtuu, jos populaation jakautuminen on täysin normaali. Kun piirretään tämäntyyppinen jakauma, se näyttää kellokäyrältä; se on symmetrinen ja suurin osa pisteistä ryhmittyy keskelle. Vino jakauma tarkoittaa yksinkertaisesti sitä, että populaation jakautuminen ei ole normaali. Datat voivat ryhmittyä esimerkiksi käyrän oikealle tai vasemmalle puolelle. Tai voi olla kaksi tai useampia pisteryhmiä, jolloin jakauma näyttää sarjalta kukkuloita.

Kun frekvenssijakaumat on määritetty, tutkijat voivat laskea keskeistendenssiä osoittavia tunnuslukuja ja hajontoja. Keskitrendimitat osoittavat jakauman keskiarvoja ja variaatiomitat osoittavat jakauman leviämistä tai vaihteluväliä.

7.2. Keskitrendin toimenpiteet

Keskitrendiä mitataan kolmella tavalla: keskiarvo, mediaani ja moodi. Keskiarvo on yksinkertaisesti jakauman keskiarvo. Mediaani on jakauman keskipiste tai keskipistemäärä. Moodi on jakauman yleisin pistemäärä. Normaalijakaumassa keskiarvo, mediaani ja moodi ovat identtiset.

7.3. Vaihtelun mitat

Vaihtelumitat määräävät jakauman vaihteluvälin suhteessa keskeisen trendin mittauksiin (keskiarvoon). Kun keskeisen trendin mittasuhteet (keskiarvot) ovat tiettyjä datapisteitä, vaihtelumitat ovat pituuksia jakauman eri pisteiden välillä tästä keskiarvosta. Vaihtelua, variaatiota, mitataan vaihteluvälillä, keskihajonnalla, varianssilla ja standardipoikkeamalla.

Vaihteluväli (range) on alimman datapisteen ja korkeimman datapisteen välinen etäisyys. Poikkeamapisteet ovat kunkin datapisteen ja keskiarvon välisiä etäisyyksiä.

Keskimääräinen poikkeama on poikkeamapisteiden absoluuttisten arvojen keskiarvo; eli keskipoikkeama on keskiarvon ja datapisteiden välinen keskimääräinen etäisyys. Keskipoikkeaman mittaan liittyy läheisesti varianssin mitta.

Varianssi osoittaa myös jakauman keskiarvon ja datapisteiden välisen suhteen; se määritetään laskemalla neliöpoikkeamien summan keskiarvo. Erotusten neliöinti absoluuttisten arvojen sijaan mahdollistaa suuremman joustavuuden laskettaessa tietojen muita algebrallisia manipulaatioita varten. Toinen vaihtelun mitta on keskihajonta.

Keskihajonta on varianssin neliöjuuri. Tämä laskelma on hyödyllinen, koska se mahdollistaa saman joustavuuden kuin varianssi lisälaskutoimituksissa ja kuitenkin myös ilmaisee vaihtelun samoissa yksiköissä kuin alkuperäiset mittaukset.

8. Ryhmien välisten erojen analysointi

Tilastollisia testejä voidaan käyttää kahden tai useamman ryhmän pistemäärien erojen analysointiin. 

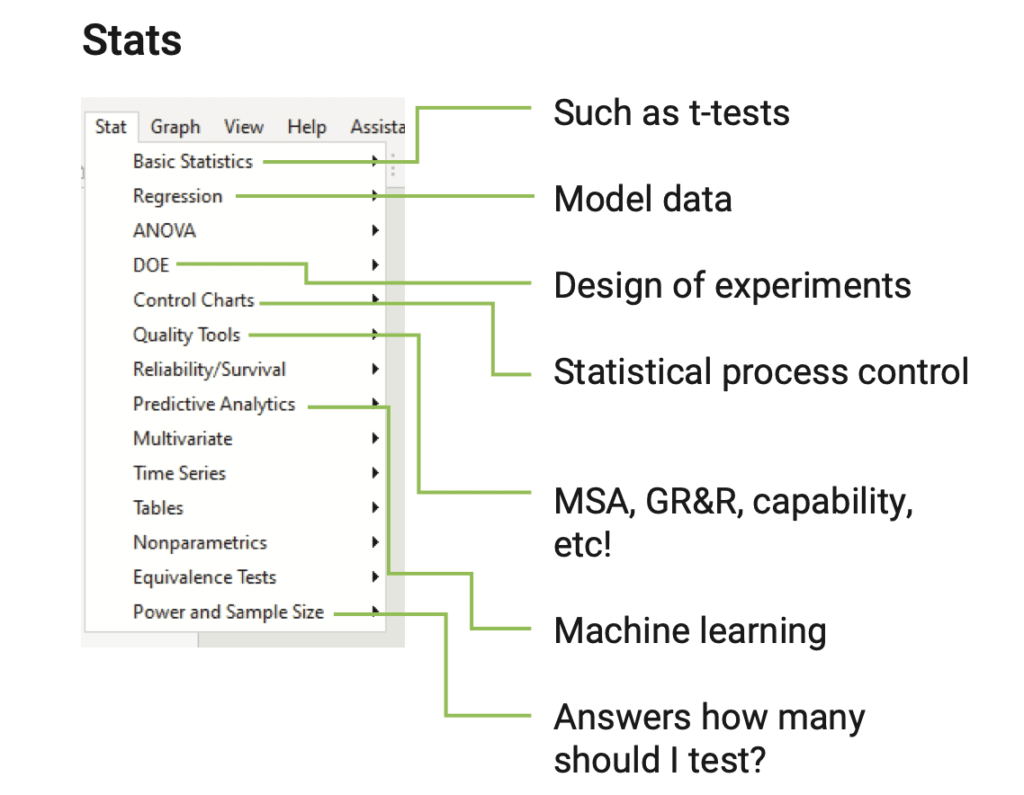
Seuraavia tilastollisia testejä käytetään yleisesti analysoimaan ryhmien välisiä eroja:

8.1. T-testi

T-testiä käytetään määrittämään, eroavatko kahden ryhmän pisteet yhdellä muuttujalla. T-testi on suunniteltu testaamaan keskiarvopisteiden eroja. Voit esimerkiksi käyttää t-testiä selvittääksesi, eroaako tuotteen jokin ominaisuus, jos muutat prosessin asetuslämpötilaa. Testiä varten sinun on kerättävä erityinen aineisto (ei siis luonnollista sattumadataa).

Huomautus: T-testi on tarkoituksenmukainen vain, kun tarkastellaan parillisia tietoja. Se on hyödyllinen analysoitaessa kahden osallistujaryhmän dataa tietyllä muuttujalla tai analysoitaessa yhden ryhmän tuloksia kahdella muuttujalla.

8.2. Yhteensopivien parien T-testi

Tämän tyyppistä t-testiä voitaisiin käyttää määrittämään, eroavatko samojen osallistujien pisteet tutkimuksessa eri olosuhteissa. Tällaista t-testiä voitaisiin esimerkiksi käyttää sen määrittämiseen, onko toinen työhöntuloreitti nopeampi kuin toinen.

Huomautus: T-testi on tarkoituksenmukainen vain, kun tarkastellaan parillisia tietoja. Se on hyödyllinen analysoitaessa kahden osallistujaryhmän pisteitä tietyllä muuttujalla tai analysoitaessa yhden osallistujaryhmän tuloksia kahdella muuttujalla.

8.3. Varianssianalyysi (ANOVA)

ANOVA (varianssianalyysi) on tilastollinen testi, joka tekee yhden kokonaisvaltaisen päätöksen siitä, onko kolmen tai useamman otoskeskiarvon välillä merkittävä ero. ANOVA on samanlainen kuin t-testi. ANOVA voi kuitenkin myös testata useita ryhmiä nähdäkseen, eroavatko ne yhden tai useamman muuttujan suhteen. ANOVAa voidaan käyttää ryhmien välisten ja ryhmien sisäisten erojen testaamiseen. ANOVA:ita on kahdenlaisia:

Yksisuuntainen ANOVA: Tämä testaa ryhmää tai ryhmiä määrittääkseen, onko yksittäisessä pistesarjassa eroja. Esimerkiksi yksisuuntainen ANOVA voisi määrittää, erosivatko fuksit, toisen vuoden opiskelijat, juniorit ja seniorit lukutaidoissaan.

Multiple ANOVA (MANOVA): Tämä testaa ryhmää tai ryhmiä määrittääkseen, onko kahdessa tai useammassa muuttujassa eroja. Esimerkiksi MANOVA pystyi määrittämään, erosivatko fuksien, toisen vuoden opiskelijoiden, juniorien ja seniorien lukutaidot toisistaan ja heijastuivatko nämä erot sukupuolen mukaan. Tässä tapauksessa tutkija saattoi määrittää (1) onko lukutaito erilainen eri luokkatasoilla, (2) onko lukutaito erilainen sukupuolen välillä ja (3) onko luokkatason ja sukupuolen välillä vuorovaikutusta.

9. Muuttujien välisten suhteiden analysointi

Muuttujien väliset tilastolliset suhteet perustuvat korrelaation ja regression käsitteisiin. Näiden kahden käsitteen tarkoituksena on kuvata tapoja, joilla muuttujat liittyvät toisiinsa (17):

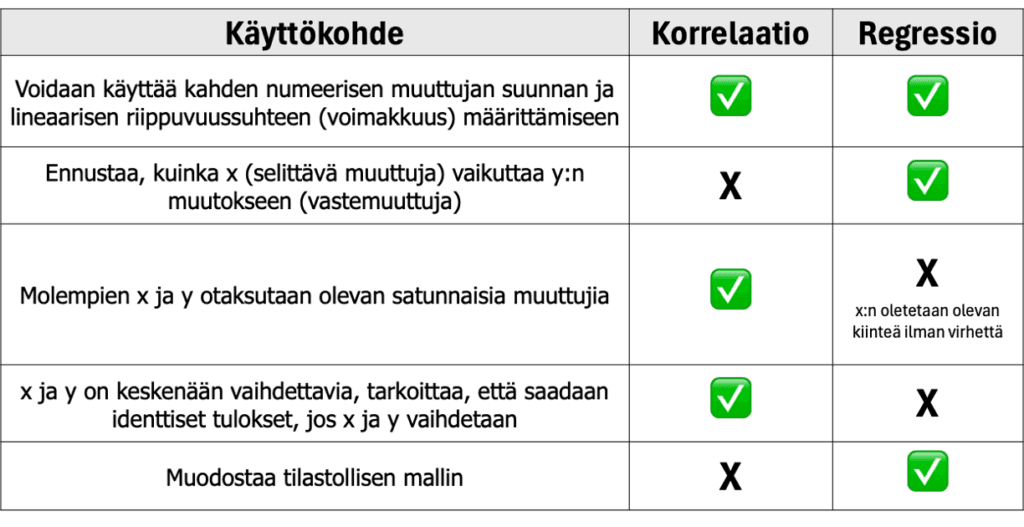
9.1. Korrelaatio

Korrelaatiotestejä käytetään määrittämään, kuinka voimakkaasti kahden muuttujan pisteet liittyvät tai korreloivat keskenään. Tutkija saattaa esimerkiksi haluta tietää, onko kahden eri valmistusaineen välillä korrelaatiota. Korrelaatio mitataan arvoilla välillä +1,0 ja -1,0. Lähellä 0:a olevat korrelaatiot osoittavat, että kahden muuttujan välillä on vähän tai ei ollenkaan yhteyttä, kun taas lähellä +1,0 (tai -1,0) olevat korrelaatiot osoittavat vahvoja positiivisia (tai negatiivisia) suhteita.

Korrelaatio tarkoittaa positiivista tai negatiivista lineaarista yhteyttä tutkimuksessa olevien muuttujien välillä. Kaksi muuttujaa liittyvät positiivisesti toisiinsa, kun toisen suurempiin arvoihin liittyy yleensä toisen suurempia arvoja. Muuttujat liittyvät negatiivisesti, kun yhden suurempiin arvoihin liittyy yleensä toisen pienempiä arvoja.

Esimerkki vahvasta positiivisesta korrelaatiosta olisi iän ja työkokemuksen välinen korrelaatio. Yleensä mitä pidempään ihmiset ovat elossa, sitä enemmän heillä voi olla työkokemusta.

Esimerkki vahvasta negatiivisesta suhteesta voi syntyä ihmisten puolueuskollisuuden ja halukkuutensa välillä äänestää eri puolueiden ehdokasta. Monissa vaaleissa kokoomuslaiset eivät todennäköisesti äänestä vasemmistopuolueita ja päinvastoin.

9.2. Regressio

Regressioanalyysi yrittää määrittää parhaan ”sovituksen” kahden tai useamman muuttujan välillä. Regressioanalyysin riippumaton muuttuja on jatkuva muuttuja, ja sen avulla voit määrittää, kuinka yksi tai useampi riippumaton muuttuja ennustaa riippuvan muuttujan arvot.

Yksinkertainen lineaarinen regressio on yksinkertaisin regression muoto. Kuten korrelaatio, se määrittää, missä määrin yksi riippumaton muuttuja ennustaa riippuvaisen muuttujan. Voit ajatella yksinkertaista lineaarista regressiota korrelaatioviivana. Regressioanalyysi tarjoaa kuitenkin enemmän tietoa kuin korrelaatio. Se kertoo, kuinka hyvin rivi ”sopii” dataan. Tämä tarkoittaa, että se kertoo, kuinka lähellä viiva tulee kaikkia tieto-/datapisteitäsi. Kuvan viiva osoittaa regressioviivan, joka on piirretty parhaan sopivuuden löytämiseksi tietopisteiden joukosta. Jokainen piste edustaa henkilöä ja akselit osoittavat henkilön työkokemuksen määrän ja iän. Pisteviivat osoittavat etäisyyden regressioviivasta. Pienempi kokonaisetäisyys osoittaa parempaa sopivuutta. Osa regressioanalyysissä annetuista tiedoista osoittaa tämän seurauksena regressioviivan kaltevuuden, R-arvon (tai korrelaation) ja sovituksen vahvuuden (osoitus siitä, missä määrin viiva voi selittää vaihtelut datapisteiden joukossa).

Usean lineaarisen regression avulla voidaan määrittää, kuinka hyvin useat riippumattomat muuttujat ennustavat riippuvan muuttujan arvon. Tutkija voi esimerkiksi tutkia, kuinka hyvin ikä ja kokemus ennustavat henkilön palkan. Mielenkiintoista tässä on, että ei enää olisi tekemisissä regression ”linjan” kanssa. Sen sijaan, koska tutkimus käsittelee kolmea ulottuvuutta (ikä, kokemus ja palkka), se käsittelee tasoa, eli kaksiulotteista hahmoa. Jos yhtälöihin lisättäisiin neljäs muuttuja, kyseessä olisi kolmiulotteinen kuvio ja niin edelleen.

10. Kokeet (experiments)

Kokeet ovat erityinen ryhmä erittäin tärkeitä tilastollisia menetelmiä, jossa suunnitellulla tavalla muutetaan tekijöitä (faktoreita). Kokeen suunnittelua ja itse koetta kutsutaankin Design of Experiments (DoE). Koesuunnitelmia on lukuisia erilaisia lähtien yksimuuttujakokeesta ja päätyen erilisiin monimuuttujakokeisiin. 

Kokeella tutkitaan tekijöiden ja ulostulon välisiä kausaalisuhteita. Kun tunnet todellisen kausaalitekijän ja suhteen, voit ehkä helpommin löytää keinon parantaa toimintaa puuttumalla tähän kausaalisuhteeseen jollain tavoin. 

Kokeista löytyy lukuisia artikkeleita QKK:n verkkosivuilta. Rajaa artikkeli ”Koesuunnittelu”, ”DoE”, ”Taguchi”, ”1-muuttuja”.

11. Täydentävät laatutekniikan työkalut

Laatutekniikka on tilastotekniikan sovellutus. Analyysin nopeuttamiseksi on tilastotekniikan menetelmiä muokattu juuri laatua palveleviksi erikoismenetelmiksi, joissa on yhdistetty erilaisia tilastotekniikan työkaluja kokonaisuudeksi. Tälläisiä ovat esimerkiksi suorituskykyindeksien laskenta, mittausten (gage) arviointi ja hyväksymistarkastuksiin liittyvät näytekokolaskennat, multivari-analyysi jne.

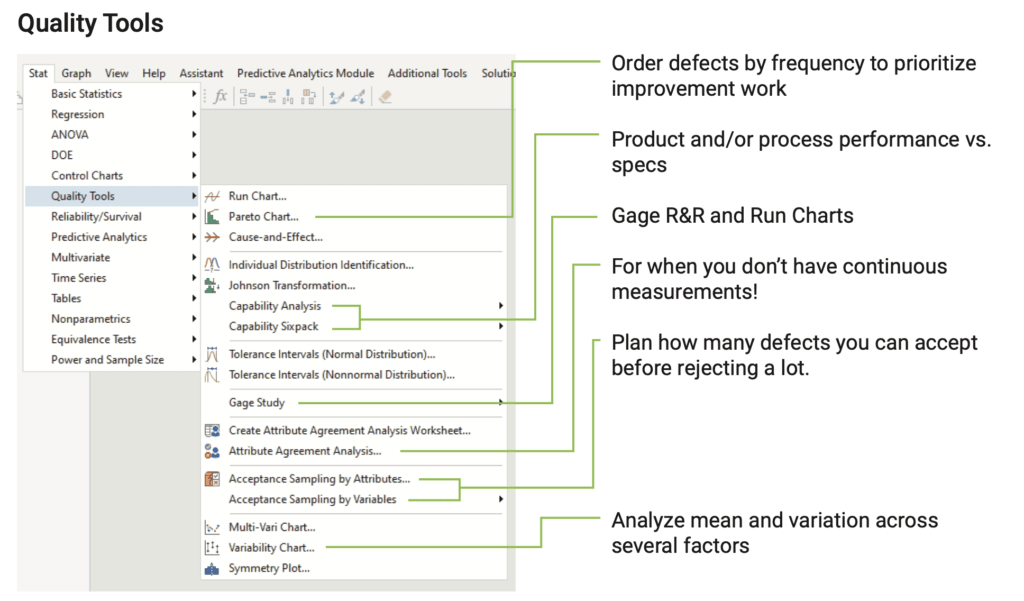
12. Tilastojen väärinkäytökset (19)

Tilastot koostuvat datan analysointiin käytetyistä analyyseistä ja testeistä. Nämä analyysit ja testit tarjoavat analyyttisen kehyksen, jossa tutkijat voivat jatkaa tutkimuskysymyksiään. Tämä viitekehys tarjoaa yhden tavan työskennellä havaittavissa olevan tiedon kanssa. 

Kuten muitakin analyyttisiä kehyksiä, tilastollisia analyysejä ja testejä voidaan käyttää väärin, mikä voi johtaa mahdollisiin väärintulkintoihin ja harhaanjohtamiseen.

Tutkijat päättävät, mitä tutkimuskysymyksiä he kysyvät, mitä ryhmiä tutkivat, miten nämä ryhmät tulisi jakaa, mihin muuttujiin keskittyä ja miten tällaisia ​​muuttujia parhaiten luokitellaan ja mitataan. 

12.1. Mahdolliset väärinkäytökset:

Manipuloiva mittakaava muuttaa tietojen esityksen ulkoasua. Asteikko voi myös olla jotain muuta kuin lineaarinen.

Eliminoimalla korkeat/matalat pisteet (erityissyyt) johdonmukaisemman esityksen saamiseksi tutkija voi vääristää tuloksia merkittävästi.

Epäasianmukainen keskittyminen tiettyihin muuttujiin ja muiden muuttujien poissulkeminen voi johtaa väärään käsitykseen syistä.

Korrelaation esittäminen syy-yhteytenä kausaliteettina on yksi yleisimmistä väärinkäytöksistä.

13. Yhteenveto

Tilastolliset käsitteet muodostavat laajan kokonaisuuden, jonka oppiminen vie aikaa. Parhaiten sen oppii tutkimalla teoriaa ja soveltamalla sitä samalla käytäntöön. Tähän tarkoitukseen Lean Six Sigma -parannuskonsepti on mitä oivallisin alusta. Samalla kun oppii tilastollisen ajattelun, menetelmät ja työkalut saa myös onnistuneesta projektista hyödyn. 

Lähteet:

1. Artikkeli: Suomalainen Laatu 2020, 2020
2. Eero E. Karjalainen, Tanja Karjalainen: Lean Six Sigma 2.0 ja laatuteknologia, 2020
3. W. E. Deming: Out of the Crisis,1982
4. Mikel Harry, Richard Schroeder: Six Sigma – The Breakthrough Management Strategy Revolutionizing the World’s Top Corporations, 2000 
5. Eero E. Karjalainen, Tanja karjalainen: Laatutaulu – Tehokas menetelmä laadunohjaukseen ja paranukseen, 2024
6. D. Wheeler kirja: Understanding Variation – The Key to Managing Chaos, 2000
7. D. Moore, G McCabe, W Duckworth, S. Sclove: The Practice of Business Statistics – Using Data for Decisions, 2008
8. Artikkeli: Prosessin ja työkoneen säätäminen ja asettaminen – OSA IV https://qkk.fi/prosessi-osa4/, 2019
9. Carlo Rovelli: Todellisuus ei ole sitä, miltä se näyttää, 2019
10. Walter A. Shewhart: Economic Control Of Quality Of Manufactured Product, 1931
11. https://www.ilmatieteenlaitos.fi/saanennustusmallit
12. Artikkeli: Seulontakokeiden tehokas käyttö, 2024
13. Andrew Sleeper: Six Sigma Distribution Modeling, 2007 
14. Matthew A. Barsalou, Joel Smith: Applied Statistics Manual – A Guide to Improving and Sustaining Quality with Minitab, 2019
15. Artikkeli: Suorituskykyanalyysit ei-normaalille datalle, 2024
16. Artikkeli: Muutanko yhtä tekijää vai useita tekijöitä? OFAT vai DoE?, 2013
17. Artikkeli: Tulkitse p:tä – mitä tilastollisilla menetelmillä on tekemistä todellisuuden kanssa?, 2022
18. Warren Chase, Fred Brown: General Statistics, 2000
19. https://wac.colostate.edu/repository/writing/guides/guide/index.cfm?guideid=67