Deduktiivinen malli                

Palvelu- ja tuotantoprosessien kyvykkyyden parantamisessa ja korjaamisessa on käytettävä eritasoisia malleja. Malli voi olla yksinkertainen ajatus: ”Kun tämän teen, niin tätä tapahtuu”. Mihin päättelyyn, tietoon tai uskomukseen, edellä oleva deduktiivinen päättely perustuu?

Tämä kirjoitus käsittelee deduktiivista mallia ja sen tarkoitus on avata, mitä tämä tarkoittaa sekä kuinka tämä helpottaa kehitys- ja/tai suunnittelutyötä.

On sanonta: ei nimi miestä pahenna, jos ei mies nimeä. Tämä koskee myös tätä termiä. Deduktiivinen malli on erittäin käyttökelpoinen ja nimeään konkreettisempi asia palvelu- ja tuotantoprosessien mallinnukseen. Tämä kirjoitus on jatkoa edelliselle kirjoitukselle, jossa kuvattiin mallien kolme luokkaa ja kuusivaiheinen prosessi analyyttiselle ongelmanratkaisuprosessille.

1. Kausaali- eli syy-vaikutus-mallinnus (Black Box), joka perustuu testeihin ja kokeisiin – joissa prosessin tekijöitä muutetaan systemaattisesti niin, että tekijöiden yksittäiset ja yhteiset vaikutukset voidaan mallintaa – Design of Experiments, DOE.  Mallia kutsutaan myös ohjaavaksi malliksi (prescriptive), jolla prosessin lukuiset ulostulot voidaan optimoida keskenään kun näihin vaikuttavat tekijät x:t. Mallin tuloksena saadaan ulostuloille (Y) ja tälle luottamusvälit halutulla virhetodennäköisyydellä. Mallin tai mallien luonti, laskenta ja optimointi tehdään Minitab-ohjelmalla. Tämä malli on Lean Six Sigman päämalli.
   
2. Korrelaatio-ennustemallinnus (Grey Box), joka perustuu satunnaisista
   palvelu- ja tuotantoprosessin havainnoista x ja samanaikaisista ulostuloista Y tehtyihin korrelaatiohavaintoihin, ei siis kokeellisesti aiheutettuihin ja tehtyihin muutoksiin, kuten kausaalimallinnuksessa. Näistä havainnoista muodostetaan prosessin korrelaatiomalli eli koneoppimisen malli (Machine learning). Mallilla voidaan simuloida ja optimoida erilaisia muuttujien (x) tilanteita ilman, että muutetaan prosessia.  Mallia kutsutaan ennustavaksi (predictive) malliksi. Mallin tuloksena saadaan ennusteet ulostulolle. Analyysitulos on esimerkiksi, että Y on 80 %:n todennäköisyydellä tämä. Malli voidaan luoda, laskea ja optimoida Minitab-ohjelmalla.
   
3. Deduktiivinen mallinnus (White Box), joka perustuu loogiseen päättelyyn lähtien peruselementeistä. Palvelu- ja tuotantoprosessien mallinnus voidaan tehdä kuudella peruskäsitteellä: kysyntä, muunnos, varasto, virtaus, bufferi ja vaihtelu. Näiden avulla niistä johdettuihin yhteyksien avulla, kuten Littlen laki, Kingmanin yhtälö, kysyntä-toimitusaikavarianssiyhtälö, voidaan muodostaa palvelu ja tuotantoprosessin kuvaava deduktiivinen malli.

Kirjoitan neljän artikkelin sarjan, joissa kolmessa viimeisessä kussakin käsitellään kutakin malliluokkaa.

Artikkeleissa kuvataan analyyttinen ongelmanratkaisuprosessi, missä yleisellä tasolla esitellään Y = f(x1…xn) mallin luomisen askeleet. Artikkelissa kuvataan askeleiden sisältö ja ideoita, mihin tätä prosessia voi käyttää. 

Ensimmäisessä artikkelissa, Analyyttisen ongelmanratkaisun kolme mallia – Osa 1, oli analyyttisen ongelmanratkaisuprosessin yhteenveto. Tämä artikkeli käsittelee vaiheet 1-6 deduktiivisen mallin sovelluksessa. 

Malli ja mallin käyttäminen

Malli (model) sanana on hankala. Me kaikki käytämme jatkuvasti malleja selvitäksemme tästä elämästä. Se onko malli oikea, onkin toinen juttu. 

Malli on tapa arvioida, mitä tapahtuu nyt ja tulevaisuudessa. Hyvän ja toimivan mallin tunnistaa siitä, että voit etukäteen tietää mitä tapahtuu, ennen kuin asia on tapahtunut. Jos näin käy, mallisi on hyvä. Toki aina tulee leegio reunaehtoja ja näiden tunteminen on osaamista. Mitä monimutkaisempi tilanne sitä tärkeämmäksi reunaehdot tulevat.

Teoreettisesta mallista lapsellisen helppo esimerkki on: tarvitset tuoremehua ja menet hankkimaan sen kauppaan. Teet oletuksen, että kaupassa on tuoremehua. Tämä ilmiselvä perusfakta on muodostunut elämäsi aikana sinulle tiedoksi.

Luot suunnitelman (todennäköisesti tiedostamatta sitä itse): kuinka käyt kaupassa, mihin kauppaan menet, mitä reittiä ja millä menet sekä arvioit, kuinka kauan matkaan menee aikaa. Varaat resurssit: ajan, rahan ja kulkuvälineen sekä aloitat suorituksen.

Saavuttuasi kauppaan valitset mehun, jonka hinta on 4,25 euroa. Sinulla on 10 euroa rahaa, etkä osta muuta, joten tiedät, että saat vaihtorahana 5,75 euroa. Toki, aina voi käydä virhe ja jos huomaat erotuksen odotusarvosta, aloitetaan virhetarkastelu. Se voi olla havainnointi-, lasku-, keräily-, hinnoitteluvirhe jne.

Malli toimii. 

Mallin käyttötarkoituksia kehitys-, suunnittelu- ja/ tai parannustoiminnassa voi olla useita. Tarkastellaan seuraavaksi vähän monimutkaisempaa tilannetta kuin edellä. Prosessi on yksivaiheinen palvelu- tai tuotantoprosessi. Lähestytään kuusivaiheisen analyyttisen ongelmaratkaisuprosessin avulla.

1. Löydä Y – nämä ovat oleellisia ulostulomuuttujia

Mallikielellä tunnista oleellinen Y. Tämä Y on prosessin ja liiketoiminnan kannalta oleellinen ulostulomuuttuja eli seuraus. Näitä Y:tä on prosessilla tai tuotteella useita ja nämä voivat olla ristiriidassa tavoitteen kanssa tai tavoitteet voivat olla ristiriitaisia keskenään. Tässä kirjoituksessa merkittävässä roolissa ovat kuusivaiheinen analyyttinen prosessi ja deduktiivinen malli, joten käsitellään vain yhtä Y:tä. 

Reaalimaailmassa mallit ovat tärkeitä etenkin tilanteissa, joissa on useita Y:tä ja useamman Y:n keskenään ristiriitaiset tavoitteet tulee saada sovitettua yhteen tai optimoitua.

Tässä esimerkissä ollaan kiinnostuneita prosessin läpi kulkevan työn ottamasta ajasta. Y on aikaa. (ks. kuva 2). Tätä muuttujaa kutsutaan operaatiotieteissä jaksoajaksi (cycle time – CT) 

Käytännön ongelma on liian pitkä ja paljon vaihteleva jaksoaika (CT), joka näkyy tuotannossa tai asiakkaalle pitkänä vasteaikana, joka vaihtelee tapauksesta toiseen. Nyt tätä ongelmaa lähestytään analyyttisen ongelmanratkaisuprosessin avulla. Y on nyt valittu.

2. Löydä X – nämä ovat oleellisia riippumattomia sisäänmenomuuttujia

Kun ongelma on tunnistettu ja valittu oleelliset Y-muuttujat, tulee kehittää oleelliset tähän vaikuttavat X-muuttujat. Nämä muuttujat ovat vaikuttavia tekijöitä, jotka saavat aikaan Y:n. Tässä vaiheessa ei yleensä tiedetä tarkkaan kaikkia vaikuttavia tekijöitä, eikä se ole mahdollistakaan.

Vaikuttavien tekijöiden valintaa lähestytään päättelemällä. Tätä lähestymistä kutsutaan päätelmäksi teoriasta.

Yleinen kuvaus (kuva 2) prosessiin vaikuttavista tekijöistä voi toimia ideoinnin apuna. 

Päättelemistä voidaan helpottaa tekemällä kuvaus käsiteltävästä asiasta. Prosessikuvaus on yksi vaihtoehto kuvata käsiteltävä asia.

Kun kuvaus on luotu, voidaan päätellä, Y:n vaikuttavat tekijät (x).

Prosessiin saapuvien töiden määrä, tyyppi ja aikaväli vaikuttaa prosessointiin ja tätä kautta se vaikuttaa jonon muodostumiseen.

Jonon koko sekä se onko jono rajoitettu vai ei, vaikuttaa jonon kokoon ja täten jaksoaikaan.

Prosessointi ja tähän kuluva aika on ilmiselvä tekijä. Käytettyyn aikaan vaikuttaa millaisia työt ovat, onnistuvatko ne kerralla, kuinka työntekemiseen kuluva normaali luontainen vaihtelu on työltä työlle, onko häiriöitä tai keskeytyksiä jne.

Tässä esimerkissä pidättäydytään yleisellä tasolla. Tähän voisi kehittää vielä paljon erilaisia tekijöitä, joista vähäisimmät eivät ole tilanteeseen vaikuttavat ulkoiset häiriötekijät, joilla on vaikutusta tarkasteltavaan jaksoaikaan.                    

3. Löydä F_Y ja F_U – Kuvaa nykytila

Seuraavaksi suoritetaan nykytilakuvaus. On tunnistettavat tekijät, joihin voidaan vaikuttaa (F_Y) ja tekijät, joihin ei voida vaikuttaa (F_U). Näitä kutsutaan ohjaus- ja häiriötekijöiksi. Jossain määrin ja käytännössä raja on häilyvä. 

Häiriötekijä on ulkoinen tekijä, johon ei voida vaikuttaa, kuten aurinko nousee idästä ja laskee länteen. Joskus voi mallinnuksessa olla halu tai tarve, että johonkin muutokseen alistutaan ja tästä päätetään tehdä häiriötekijä. Esimerkiksi joskus kysynnän vaihteluun voitaisiin vaikuttaa, mutta päätetään, että ei haluta aloittaa asiakkaan ohjaamista.

4. Löydä Y = f(x) – Kuinka Y ja X liitetään toisiinsa

Ulostulomuuttujien eli seurausten ja riippumattomien sisäänmenomuuttujien yhteys voidaan luoda eri keinoin. Malli voidaan luoda satunnaistetulla kokeella. Näin luotua mallia kutsutaan Black Box -malliksi – kausaalimalli. Malli voidaan luoda myös havaintotutkimustiedosta eli käytännössä aiemmin kerätystä aineistoa analysoimalla. Tätä kutsutaan Grey Box -malliksi eli korrelaatiomalliksi. 

Tässä esimerkissä käytetään operaatiotieteissä käytettyä mallia. Malli on deduktiivisesti johdettu yleisestä teoriasta eli White Box -malli.

Prosessin jaksoaika (CT) on jonotusaika (CT_q) plus tehollinen prosessointiaika (t_e). Missä jonotusaika = V*U*T. VUT yhtälö tunnetaan myös nimellä Kingmanin yhtälö. Prosessointiaika on todellinen toteutunut keskimääräinen prosessointiaika yhtä kappaletta kohden. 

Kuvassa 5 on esitelty malli ja aiemmin kehitetyt muuttujat.

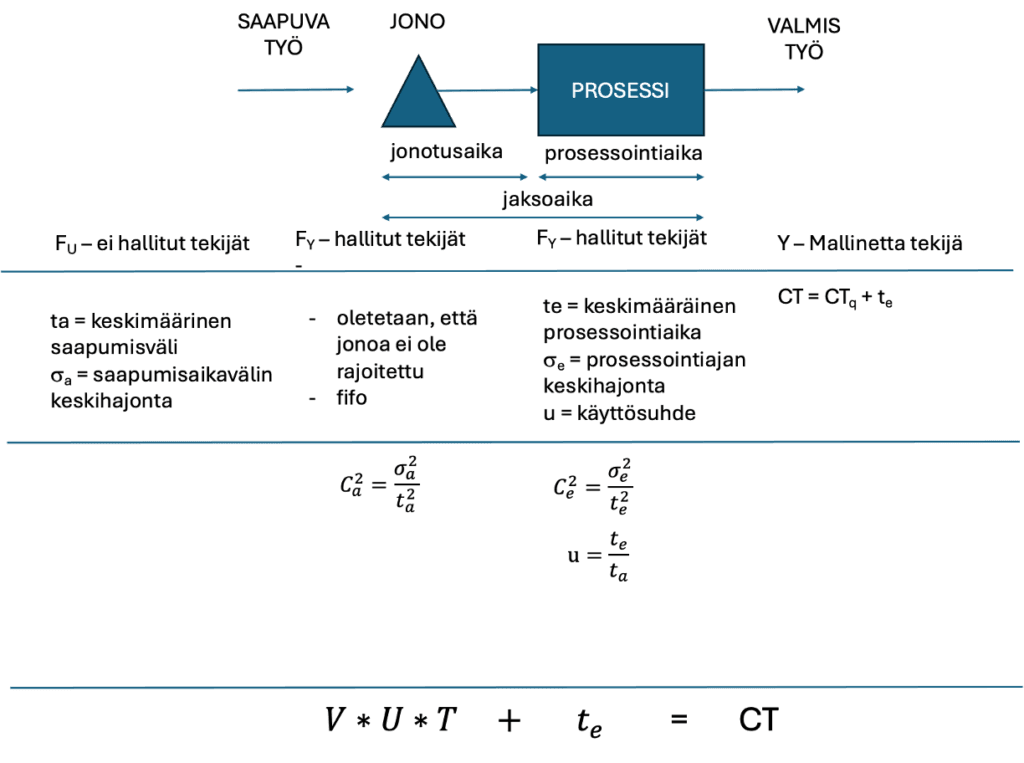
Valitussa deduktiivisessa mallissa olevat parametrit:

• t_a ja σ_a kuvaavat prosessin kohdistuvaa saapuvaa työmäärää ja sen vaihtelua. t_e ja σ_e kuvaavat prosessointia, missä varsinainen työ tehdään ja mikä purkaa jonoa.

• C_a² ja C_e² ovat laskennallisia neliöllisiä vaihtelukertoimia, jotka VUT-yhtälössä auttavat arvioimaan tarkastelun kohteena olevaan kohteeseen vaikuttavan vaihtelun vaikutusta jonoutumiseen. 

• u on käyttösuhde, joka kuvaa todennäköisyyttä, kuinka kiireinen prosessi on. 

Nämä mallissa olevat parametrit voidaan pilkkoa vielä pienempiin osiin. Tässä esimerkissä jätetään ne tälle tasolle. Palataan kuitenkin näihin tässä kirjoituksessa myöhemmin.

Kun malli (f(x)) on valittu ja parametrit (x) tunnistettu, voidaan selvittää kuinka prosessissa olevat tekijät vaikuttavat ulostuloon (Y).

5. Löydä V(Y, X^C, F^U) – Mikä on tavoite

Mallin avulla tutkitaan, kuinka päästään tavoitteeseen. Tavoitteena on löytää, millä X^C eli ohjattavien tekijöiden tasolla haluttuun tavoitteeseen päästää ja mitä tämä vaatii.

Mallinnettavilla kohteilla on tavoitteita, jotka voivat olla ristiriidassa. Operaatioista tyypillisenä esimerkkinä lyhyt vasteaika on tavoite, joka vaatii ylimääräistä kapasiteettia. Toisaalta tavoitteena voi olla saman aikaa maksimoida kapasiteetin käyttö. Tarvitaan arvofunktio (Y, X^C, F^U), minkä avulla arvotetaan kapasiteetti ja vasteaika.

Tässä esitellyssä yksinkertaisessa tilanteessa keskitytään yhteen asiaan eli jaksoaikaa, jonka malli on:

Jonotusaika (VUT) + prosessointiaika (te) = jaksoaika

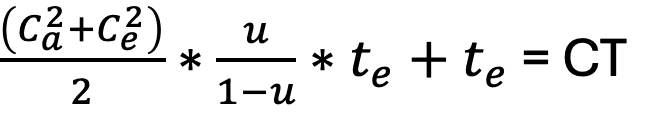
Kuvassa alla on kehitetty luvut malliin ja laskettu muodostuva jaksoaika. Laskennan tulosta verrataan reaalimaailman tilanteeseen. 

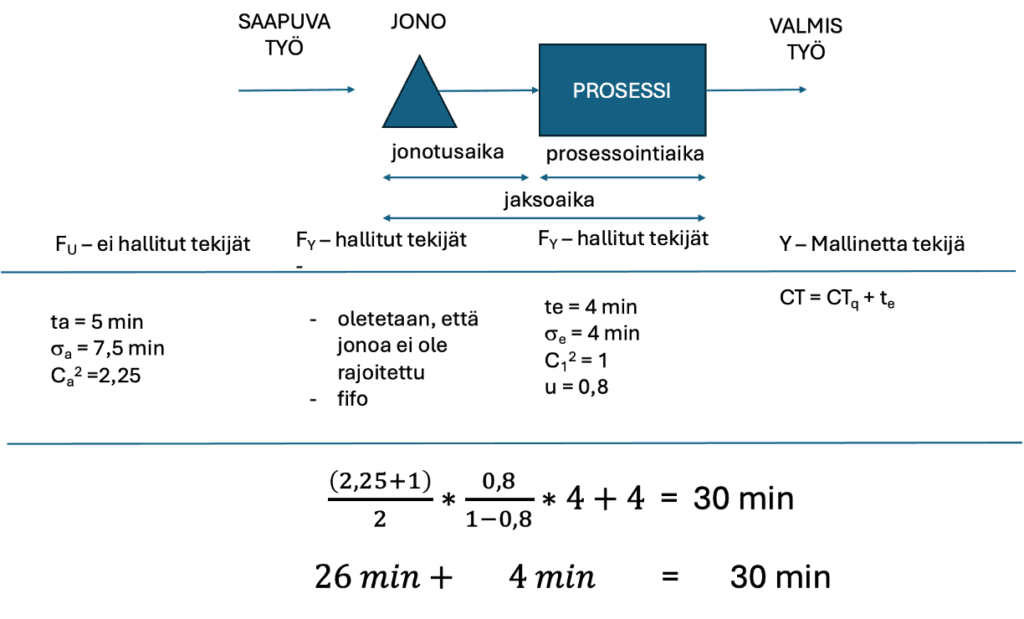
Tavoitteena on puolittaa jaksoaika (CT). Tässä esimerkissä oletetaan, että saapuvalle työlle ei haluta tehdä mitään, koska kysyntää ei haluta rajoittaa. Esimerkissä ei myöskään käsitellä vaihtelua (σ_e).

Oletetaan, että tutkimuksessa havaittu keskimäärinen 4 min per työ koostuu seuraavista ajoista. Varsinainen työn tekeminen kestää 2,5 min per työ, laatuongelmat ovat 0,5 min per työ, laitevika 0,4 min per työ, osaamattomuus 0,3 min per työ, häiriöt 0,2 min per työ ja muut tekemisen esteet 0,1 min per työ eli yhteensä 4 minuuttia per työ.

6. Löydetään paras ratkaisu V(Y, X^C, F^U) – Kuinka tilanne on ratkaistu

Mallin ja siinä olevien hallittavien tekijöiden avulla voidaan hakea optimiratkaisu. Jos oletetaan, että jaksoajalle tavoite on 15 minuuttia ja kysyntään ei saa koskea, voidaan yhtälöstä ratkaista t_e, millä päästään tavoitteeseen. Asetetaan Y:lle 15 min ja ratkaistaan t_e.

Toki vaihtelun tutkiminen olisi myös mahdollista, mutta tässä esimerkissä pidetään tilanne yksinkertaisena ja haetaan prosessointiaika, jolla päästään puolet lyhyempään jaksoaikaan.

Muistetaan, että prosessointiaika koostuu erilaisista tekijöistä ja näihin vaikuttaminen on erihintaista ja vaikeudeltaan erilaista. Oletetaan myös, että vaihtelu pienenee samassa suhteessa, kuin työn tekemisen aika.

Optimoinnin voisi suorittaa millä tahansa laskentaohjelmalla, kun tiedetään ajan osakomponentit ja niihin vaikutusmekanismit sekä arvioit, vaikka kustannuksesta.

Ratkaisu on t_e = 3,28 min per työ. Tämä on 0,72 min per työ lyhyempi kuin alkuperäinen aika.

Todetaan aikojen perustella, että tilanteessa laatuongelmat ovat yksi isoimmista, joten ajatellaan sen olevan toimenpide kohde. Toinen suuri osatekijä on erityyppiset häiriöt, joiden todettiin johtuvan työpaikalle pesiintyneestä työn keskeyttämisen kulttuurista. Laiteviat paljastuivat ohjelmistopäivityksiksi, jotka voidaan ajastaa tapahtuvan työajan ulkopuolella.

Lopuksi huomataan, että itse työ on jäänyt vuosiksi kehittämättä. Joten tästä saadaan myös merkittävästi aikaa lyhyemmäksi.

Arvioitiin, että työn tekeminen lyhenee 2,5 min -> 2,2 min, laatuvikoja poistamalla lyhenee aika 0,6 min -> 0,3 min, laiteviat 0,4 min -> 0,3 min, häiriöt 0,2 min -> 0,1 min. Kokonaisuudessa nämä lyhentävät tekemiseen käyttävää aikaa noin 0,7 min per työ ja uusi prosessointiaika on 3,4 min per työ.

Päätettiin myös, että osaamattomuus ei ole merkittävä ongelma, vaan se on hyväksytty tosiasia. Tässä työpisteessä käydään välillä tuuraamassa toisia, joten väistämättä tulee uusia asioita esiin. Tämän hyväksyminen tukee myös muuten toimintaa, koska se kasvattaa moniosaamista.

Deduktiivisen mallin huono puoli on, että sen avulla ei voida arvioida Y:lle kuin keskiarvo. Kuten esimerkistä voidaan havaita, on muodostuva 15 minuutin jaksoaika keskiarvo ja ei ole mitään keinoa arvioida yksittäisen työn ottamaa aikaa prosessin läpi.

Lopuksi

Kirjoituksessa käytetty esimerkki on yksinkertainen ja yksinkertaistettu. Tarkoituksena oli esitellä analyyttistä ongelmanratkaisuprosessia ja kuinka esitelty kuusivaiheinen analyyttinen ongelmanratkaisuprosessi tukee ratkaisun löytymistä.

Vuonna 2013 esiteltiin Quality Progress -lehdessä kuvassa 8 oleva nelikenttä. Olen tätä liki kaikissa koulutuksissa pitänyt esillä, jotta erilaiset ongelmatilanteet jäsentyvät. Ongelmat ja keinot ovat erilaisia. Lääkärin tavoitteena on saada terve ja työkykyinen henkilö. Tämän jälkeen tulee tehdä diagnoosi ja tämän jälkeen tulee keinot. 

Kuvassa 8 esitellysti ongelma voi olla yksikertainen ja ratkaisu on tunnettu, jolloin toiminta on Just do It. Liiketoiminnan kannalta kysymys on, miten se tunnistetaan ja kuinka se hoidetaan, jos tarve on tehdä jotain.

Toiminta voi olla myös erityissyy normaalista poikkeava tilanne, missä ratkaisu ei ole tunnistettu. Tällöin tarvitaan ongelmanratkaisukeinoja selvittämään yksitäistä tilannetta ja pohtimaan mikä on muuttunut.

Nelikentän oikea alalaita käsittelee tilanteita, missä ei ole mitään merkittävää poikkeamaa olemassa, mutta suorituskyky ei vaan riitä ja ratkaisu on tuntematon. Tähän käytetään Six Sigmaa ja kausaalimalleja eli Black Box -malleja.

Nelikentän vasen alalaita kuvaa monimutkaista tilannetta, missä ratkaisu on tunnettu. Näitä käsitellään esimerkiksi operaatiotieteissä ja tähän sopii eriomaisesti deduktiiviset mallit. Malleja on paljon ja soveltamiskeinoja on paljon.

Tämän artikkelin tarkoituksena oli esitellä analyyttinen ongelmanratkaisuprosessi ja sen vaiheet 1-6 sekä kuvata, mitä deduktiivinen malli voi tarkoittaa. Lisäksi esiteltiin, kuinka yksinkertainen Kingmanin yhtälö auttaa ymmärtämään vaikutussuhteita ja määrittämään, kuinka tavoitteeseen päästään.

Esimerkistä opittavaa on, että prosessointiaikaa lyhentämällä (olkoon keino mikä tahansa), prosessointinopeus kasvaa ja käyttösuhde laskee, joka taas laskee muodostuvaa jonotusaikaa. Noin 0,7 minuutin lyhennys prosessointiaikaa lyhensi 15 minuuttia jaksoaikaa.

Deduktiiviset mallit auttavat prosessin vaikuttavien tekijöiden tunnistamisessa, syy-seurausyhteyksien ymmärtämisessä sekä parannustoimenpiteiden vaikuttavuuden arvioinnissa.

Me kaikki käytämme malleja ja seikkailemme monimutkaisessa pirstaloituneessa tietomaastossa niin kotona kuin töissä. Hyvä malli auttaa, huono sekoittaa ja ohjaa väärin. 

Lähteet:

1. J. D. Mast, S. H. Steiner, W. P. M. Nuijten & D. Kapitan. 2022. Analytical Problem Solving Based on Causal, Correlational and Deductive Models
2. Roger W. Hoerl ja Ronald D. Snee: One Size Does Not Fit All – Identifying the right improvement metodology, Quality Progress, May 2013
3. W. J. Hopp, M. L. Spearman: Factory Physics, Third Edition, 2008