Bayes ”puhuu” meille tapahtumien syiden todennäköisyydellä, totuudesta?

Olemme Covid-19 -viruksen testauksen yhteydessä törmänneet tietämättämme pastori Bayesiin ja testatun syyn (taudin) selvittämisen vaikeuteen. Kysymys on testaustuloksen ja taudin/vian välisestä kausaliteetin todennäköisyydestä. Voitko testitulokseen luottaa?

Tämä syyn ja seurauksen ongelma on edessä myös jokaisella reklamaatioita, valituksia tai ongelmien syitä selvittävällä. Mikä on totuus? Kertooko positiivinen testi- ja mittaustulos sairauden, ongelman tai virheen olemassaolosta ja kääntäen tarkoittaako ”puhdas” negatiivinen tulos terveyttä, ongelmattomuutta tai virheettömyyttä? Tämän selvittämiseksi on tiedettävä, mikä on mittauksen taudin ja virheen/vian esiintyvyystodennäköisyys (taajuus).

Testauksen ja mittauksen virhe muodostuu kahdesta virhelähteestä, tarkkuudesta/spesifisyydestä (accurancy) ja herkkyydestä/täsmällisyydestä (precision). Kysymys on luokittelusta ja attribuutti MSA-menetelmästä (Measurement System Analysis), jolla mittausvirhe voidaan määrittää ja jakaa komponentteihin.

Herkkyys/täsmällisyys prosentti (0-100%) tarkoittaa testausmenetelmän kykyä ilmaista sairaus tai virhe/vika, kun tiedetään sairauden/virheen/vian olevan kohteessa 100%:n varmuudella. Tarkkuus/spesifisyys prosentti (0-100%) ilmaisee tuloksen oikeellisuutta (siis negatiivinen tulos), kun sairautta/vikaa/virhettä ei ole 100%:n varmuudella kohteessa. Taulukko 2.

Koronan testaukseen ei vielä ole laajasti hyväksytty antigeeniin perustuvaa pikatestausta, jossa tuloksen saa puolessa tunnissa, koska testin herkkyys ei ole riittävä (<80-95%). Sen sijaan ”hyväksyttyyn” testaukseen käytetään viruksen perimän monistukseen (vahvistukseen) perustuvaa PCR-testiä, jossa tuloksen saamiseen saattaa kulua jopa useita päiviä, mutta testin herkkyys on lähes 100% analyysin osalta. Miksi antigeenitestin herkkyys ei riitä, mitä siitä seuraa?

Thomas Bayes ja hänen teoriansa, joka ”estää” koronapikatestit

Thomas Bayes (1702-1761) oli maallikko pappi, joka oli ”matematiikkanörtti”. Bayes asetti teologian ja matematiikan vastakkain ja loi Bayesin kaavan tai säännön. Kuva 1

”Laatu”pastori Bayes halusi todistaa matematiikan keinoin Kristuksen ylösnousemisen kuolleista. Filosofi David Hume oli Ihme -esseessään vuonna 1748 väittänyt ylösnousemuksen olevan epätosi: ”Silminnäkijän lausunto ei koskaan voi todistaa ihmeen tapahtuneen. Luonnostaan erehtyväiset todisteet eivät koskaan kumoa luonnonlakiin perustuvia väitteitä – kuolleet pysyvät kuolleina.”

Pastori Bayes esitti kysymyksen: kuinka paljon tarvitaan todisteita vakuuttamaan meidät siitä, että epätodennäköisenä pitämämme todella tapahtuu? Milloin hypoteesi ylittää mahdottoman ja epätodennäköisen rajan ja muuttuu jopa todennäköiseksi tai käytännössä varmaksi?

Tämän saman kysymyksen eteen joutuu jokainen tauteja, reklamaatioita tai ongelmia selvittävä laatuammattilainen kuin myös parannusten ja Leanin ja Six Sigman kanssa työskentelevät. Näet seurauksia, mutta mikä on kausaalisyy tai ”idea” parannukseen? Mikä on syyn tapahtuman todennäköisyys, jotta voit pitää sitä totena ja parantaa sillä tai siihen vaikuttamalla? Kuinka paljon ja millaista todistusaineistoa etsit ja esität asialle tai tapahtumalle, jonka väität jonkin asian syyksi vai esitätkö vain oman mielipiteesi! Tarkemmin kausaliteetista artikkelissani: Kausaliteetti-syy ehto parannukselle – mitä se on?

Bayes osoitti, että syyn todennäköisyys voidaan päätellä seurauksista (so. testituloksesta). Tätä sanotaan käänteiseksi todennäköisyydeksi, prioritodennäköisyydeksi. Jos sen sijaan syy tiedetään, on helppo arvioida vaikutuksen todennäköisyys. Tätä sanotaan posterioritodennäköisyydeksi tai klassiseksi todennäköisyydeksi tai frekvenssitodennäköisyydeksi.

Jos esimerkiksi tiedät, että pojat heittelevät ulkona ikkunoihin kiviä ja joka kymmenes ikkuna särkyy kivestä, saat selville posterioritodennäköisyyden P(K) =1/10. Mutta jos olet sisällä ja tiedät poikien heittelevän sekä tennispalloja että kiellettyjä kiviä, voit yrittää määritellä seurauksista ikkunan särkymisen prioritodennäköisyyttä, joka on aiheutunut kivestä. (Tennispallolla rikkominen on tietysti ”sallittu” vahinko!)

Bayesin sääntö

Bayesin säännön ymmärtämiseksi oletetaan, että pihalla on 12 poikaa, joista osa (2/3, 66%) heittelee tennispalloa (T) ja pienellä osalla näistä pojista on kiellettyjä kiviä (K) (1/2, 50% ), joita he heittelevät ikkunoihin. Tästä voidaan helposti laskea, että pihalla on 12*2/3*1/2=4 poikaa (33%), jotka heittelevät tennispalloja ja kiviä. Muodostetaan tennispallon ja kivenheitosta satunnaistaulukko.

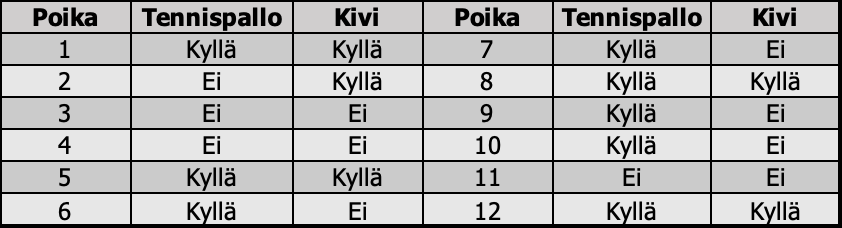
Taulukosta 1 nähdään 12 pojan heittovälineet pihalla – 2/3 heittää palloa (1, 5, 6, 7, 8, 9, 10, 12) ja ½ heistä myös kiviä (1, 5, 8, 12). Pallo ja kivi ½ *2/3=1/3=4, kuten ennustimme.

Bayesin säännön lähtökohta on huomata, että aineiston olisi voinut analysoida käänteisessä järjestyksessä! Miten?

Lähdetään kivistä K (ikkunan rikkoutumissyystä). Havaitaan, että viisi kahdestoistaosaa (5/12, 41%) heittää kiviä ja heistä neljä viidesosa (4/5, 80%) heittelee myös palloa. Niinpä palloa ja kiviä heittelee 4/5 *5/12=1/3 =4, kuten edellä huomasimme.

Yleistämme edellä olevan säännön merkitsemällä, että

• P(T) pallon heittämisen todennäköisyys (2/3, 66%)
• P(K) kiven heittämisen todennäköisyys (5/12, 41%)
• P(K|T) kiven heittämisen todennäköisyys ehdolla, että pojalla on pallo (1/2, 50%)
• P(T|K) pallon heittämisen todennäköisyys ehdolla, että pojalla on kivi (4/5, 80%)

Tästä saamme todennäköisyyden kiven ja pallon heittämiselle kahdesta eri suunnasta, kausaalisuunnasta ja ei-kausaalisuunnasta

P(K ja T) = P(K|T)*P(T)

P(T ja K) = P(T|K)*P(K)

Tästä saadaan edelleen Bayesin kaava tai Bayesin sääntö

Kaavasta nähdään, että se esittää yleisen ratkaisun käänteiseen todennäköisyyden ongelmaan.

Yleinen käänteinen todennäköisyys tarkoittaa, että jos tiedetään todennäköisyys K ehdolla T eli P(K|T), voidaan päätellä todennäköisyys T ehdolla K eli P(T|K), kun oletetaan, että tiedetään todennäköisyydet P(T) ja P(K).

Tilastotieteessä Bayesin säännöllä voidaan arvioida suoraan ehdollinen todennäköisyys yhteen suuntaan, jossa arviointikyky on luotettavampi ja sen jälkeen johtaa ehdollinen todennäköisyys toiseen suuntaan, jossa arviointikyky on hämärämpi.

Oletetaan ikkunan rikkoutumisen esimerkki, jossa kysyttiin todennäköisyyttä, että poika, jolla on tennispallo ja kivi, rikkoo ikkunan. Kysymys: Mikä osa pojista on tennispallo ehdolla kivi P(T|K)? P(T|K)*5/12=1/2*2/3 => P(T|K)=4/5 (80%)

Bayesin sääntöä voidaan pitää myös keinona ”päivittää” uskoa tiettyyn hypoteesiin. Suuri osa ihmisistä uskoo tuleviin tapahtumiin perustuen taajuuteen/esiintyvyyteen, jolla ne tai samankaltaiset tapahtumat ovat aikaisemmin esiintyneet. Tämä voidaan päivittää oikeaksi todennäköisyydeksi virheuskomuksen sijaan. Bayesin sääntöä voidaan pitää myös keinona päivittää uskoa tiettyyn hypoteesiin.

Tennispallon heittelyn frekvenssitodennäköisyys on P(T)= 2/3 ja tennispallon heittelyn todennäköisyys kiven ehdolla on P(T|K)= 4/5.

Bayesin sääntö väittää K:n uskottavuus T:n havaitsemisen jälkeen P(K|T)= 4/5 ei ole koskaan pienempi kuin suureen P (K JA T) uskottavuusaste P(K|T)*P(T) = 4/5*2/3=8/15 T:n havaitsemisen jälkeen (P(K|T)= P(T|K)*P(K)/P(T) > P(K|T)*P(T))

Mitä yllättävämpi todiste T on, sitä pienempi P(T) on ja sitä vakuuttuneempi tulee olla siitä, että K on sen syy. Tällä perusteella Bayes vastasi Humelle: Jos T on ihme (”Kristus nousi kuolleista”) uskomuksen aste hypoteesiin K kasvaa dramaattisesti (K = ”Kristus on Jumalan poika”), jos tiedämme, että T on tosi. Mitä ihmeellisempi on ihme (nousta kuolleista), sitä uskottavampi on hypoteesi, joka selittää sen.

Lääketieteellisten testien tarkkuus ja herkkyys

Palataan Covid-19:sta. Teetät lääketieteellisen kokeen T selvittääksesi, onko sinulla tietty sairaus D eli aiheuttaako sairaus testituloksen (kausaliteetti). Oletetaan, että tulos on positiivinen. Kuinka todennäköistä on, että sinulla on sairaus?

Posterioritodennäköisyys on positiivisen tuloksen todennäköisyys ehdolla, että on sairaus: P(testi|sairaus). Tätä lääkäri tarkoittaa, kun puhuu ”testin” herkkyydestä tai kyvystä havaita sairaus oikein (kausaalisuus). Herkkyys riippuu VAIN laitteesta (testistä)! Antigeenitesteillä tämä on 0-94%:n luokkaa. Eräs antigeenitesti varmentuu PCR-testeillä vain 56%:sti eli ehkä vajaa puolet koronaa sairastavista paljastuu (HS 4.9.2020).

Käänteinen todennäköisyys (prioritodennäköisyys) kiinnostaa kuitenkin potilasta enemmän: Mikä on todennäköisyys, että sairastan, kun testin tulos on positiivinen? P(sairaus|testi)? Tämä kuvaa informaation virtaa ei kausaaliin suuntaan – testin tuloksesta sairauteen. (Tämä ei ole kaikilla potilailla sama kuten on herkkyydessä). Huomaa, että nyt puhutaan kahdesta suunnasta – kausaalista ja ei kausaalista.

Valaistaan tätä esimerkillä, joka on professori Judea Pearlin kirjasta Miksi – syyn ja seurauksen uusi tiede: Oletetaan, että 40-vuotias nainen käy mammografiassa selvittämässä, onko hänellä rintasyöpä – ja tulos on positiivinen? Hypoteesi on D (sairaus, disease), hänellä on syöpä! Todiste T (”testi”) on mammografian tulos. Kuinka vahvasti hänen tulee uskoa hypoteesiin? Tuleeko mennä leikkaukseen?

Vastataan kirjoittamalla Bayesin sääntö seuraavalla tavalla:

Päivitetty P(D|T) = todennäköisyyssuhde (Odds) * P(D):n prioritodennäköisyys

Lausekkeessa on uusi termi ”todennäköisyyssuhde, Odds” P(T|D)/P(T). Todennäköisyyssuhde (odds) mittaa, kuinka paljon todennäköisempi on positiivinen testitulos sairastuneilla kuin positiivinen tulos koko väestössä. Uusi todiste T kasvattaa D:n todennäköisyyttä kiinteällä suhteella prioritodennäköisyydestä P(D) riippumatta.

Tarkastellaan 3000 henkilön rintasyöpätestiä. 40 vuotiaan naisen todennäköisyys sairastua syöpään USA:ssa on 1/700=0,14%. Tämä on prioritodennäköisyys P(D). Todennäköisyys-suhteen laskemiseksi on tiedettävä P(T|D) ja P(T). Lääketieteessä herkkyys P(D|T) 40 vuotiaiden syöpätestien tiedetään olevan 73%. P(T) positiivinen testitulos saadaan sekä sairastuneilta että terveiltä. Positiivinen tulos tiedetään olevan P(T)=1/700*73 % + 699/700*12%= 12,1 % (363). Kun tiedetään P(T), voidaan laskea todennäköisyyssuhde odds 73/12,1=6. Tästä saadaan päivitetty todennäköisyys sairastaa syöpää =6*1/700=0,85% (3 sairastunutta). Tulos on hämmentävä. Positiivisen testituloksen saaneista (363) vain alle 1 % (3 ) sairastaa syöpää (katso kuvaa 2).

Esimerkki perustuu Brest Cancer Survelliance Concortiumin antamiin väärien negatiivisten ja väärien positiivisten määriin, vain 3 363:sta 40 vuotiaasta, jotka saivat positiivisen tuloksen rintasyöpätestissä, todella sairastaa syöpää. Lähde: Judea Pearl, Miksi – syyn ja seurauksen uusi tiede, sivu 114.

Covid-19 -virustestien osalta P(D) vaihtelee pandemian levitessä ja minä hetkenä sairautta virusta testataan. Suomessa P(D) on tällä hetkellä 0,02-1% luokkaa. P(T) voidaan määrittää eräälle antigeenitestille, jolle on ilmoitettu herkkyydeksi P(T|D)=94% ja tarkkuudeksi 95%, kun sairautta esiintyy 1%. P(T)=(0,01*0,94 + 0,05*0,99)/100=5,89. (HS 7.5.2020). Odds-suhde 94/5,89=15,9. (Karkeasti todennäköisyyssuhde Odds ≈ Herkkyys%/(100-Tarkkuus%)=18,8). Taulukko 2.

Päivitetty todennäköisyys sairastaa koronaa antigeenitestin perusteella on P(D|T) ≈ 15,9*1%=15,9%! Taudin oireselvityksellä – omaolo.fi tai lääkäri – voidaan P(D):tä ”nostaa” 100% esimerkiksi 2%:iin, jolloin päivitetty P(D|T) nousee n. 28%:iin.

Tuote- ja lopputarkastuksen tehokkuus – tarkkuus ja täsmällisyys

Edellä esitetty esimerkki on suoraan sovellettavissa tuote- ja lopputarkastuksen luokitteluun hyviin ja huonoihin. Tyypillisesti tarkastusten oikeellisuus on teollisuudessa alle 30% ja jopa paljon alle – puhdasta ”arvontaa”. Miten tehdä huippulaatua minimikustannuksin ilman erottelevaa tuotetarkastusta?

Suorituskyvyn parantaminen on avain huippulaatuun minimikustannuksin – ja päästään eroon tarkastusperusteisesta toiminnasta kohti varmentavaa tarkistusta. Tarkastamalla ja erottelemalla voidaan saada aikaan vain huonoja tai korkeintaan keskinkertaisia tuotteita ja palveluja!

Uusin kirjamme johdattaa suorituskyvyn parantamiseen ja käytettyihin menetelmiin: Lean Six Sigma 2.0 ja Laatuteknologia. Kirjassamme käsitellään Lean Six Sigmaa ja siihen liittyvää laatuteknologiaa, jolla voidaan parantaa niin mittauksen kuin prosessien suorituskykyä ja säästää kustannuksia.

Ennen suorituskykyperusteiseen toimintaan siirtymistä on hyvä määrittää tarkastuksen hyvyys ja kyky erotella ja poimia viat (”taudit”). Tämän määrittämiseksi on tiedettävä tarkkuus ja täsmällisyys (lääketieteessä spesifisyys ja herkkyys) ja tämän jälkeen parannettava mittausprosessi lähelle 100%:a. Testaus/mittausvirheen määrityksen voi tehdä parhaiten käyttämällä hyväksi attribuutti MSA-menetelmiä ja itse mittausprosessin suorituskyvyn parannuksen käyttämällä Six Sigman DMAIC-menetelmää.

Minitab 19:ssä on Assistant, jolla määritystestin luonti ja analyysi ja laskennat voi toteuttaa helposti. Tätä käsitellään Lean Six Sigma -kursseilla DMAIC-prosessissa (Define, Measure, Analysis, Improvement, Control). Mittausta opetetaan myös QKK:n erillisillä mittaustekniikan kursseilla.

Bayes ja tieteellinen menetelmä

Bayesin menetelmä kiteyttää oivallisesti tieteellisen menetelmän, jolla kausaliteetti, syyn prioritodennäköisyys, voidaan selvittää (Six Sigma, DOE)

1. Muodostetaan hypoteesi
2. Päätellään hypoteeseistä testattavat seuraukset
3. Tehdään koe ja kerätään todisteita
4. Päivitetään uskomus hypoteesiin

Bayesin sääntö kertoo, miten proseduuri käännetään päinvastaiseksi erityisesti kertomalla prioritodennäköisyys todennäköisyyssuhteella! Tämä suhde saadaan esimerkiksi koetuloksen vastekuvista ja vaikutustaulukoista (contribution %).

P(S|T) = todennäköisyyssuhde (odds)*P(S)
              -todennäköisyyssuhde, odds-suhde = P(T|S)/P(T) ≈ Herkkyys%/(100-Tarkkuus%)

Yhteenveto

Bayes puhuu meille syiden todennäköisyydellä, kausaliteetilla. Ihmisillä on taipumus puhua ja uskoa tapahtumien esiintymisen (tiheyden) todennäköisyyksiin tässä ja nyt. Bayesin sääntö ”korjaa” ihmismielen vinoumia totuuden mukaisiksi – ja mahdollistaa huippulaadun.

Mittaus/testaus/havainto ja sen hyvyys on kriittistä niin lääketieteessä kuin myös tuotteita ja palveluja tehtäessä. Usein uskotaan, että mittaus ja testi ovat aina oikeita ja pystyvät erottelemaan hyvän huonosta 100%:sti. Näin ei kuitenkaan ole. Kun esiintyvyys laskee alle 10-20%:n prosentin, mittauksen tarkkuus/spesifisyys ja täsmällisyys/herkkyys tulevat kriittisiksi tekijöiksi ja samalla merkittäviksi kustannustekijöiksi. Kausaalisyyt alkavat ”hämärtyä” ja virhetulokset sotkevat totuutta.

Jokaisen testin/mittauksen tarkkuus ja täsmällisyys/herkkyys olisi selvitettävä erityisesti silloin kun vian tai sairauden esiintyvyys on pieni. Kuten Covid-19 -virus on osoittanut, testaaminen (näytteenotto, analyysi) on vaativaa luotettavan tuloksen aikaansaamiseksi – ja kallista. Suomikin käyttää 1,4 miljardia euroa vuosittain Covid-19 -testauksiin (HS 11.9.2020) ja tulokseksi saadaan tautiepäilyjä ja epävarmuutta. Vain rokote ja korkea palveluiden ja tuotteiden suorituskyky (ennaltaehkäisy) tarjoaa ulospääsyn pienen esiintyvyyden ongelmista ja epävarmuudesta. Testaus/tarkastus ei tätä ratkaise!

Pastori Bayes osoitti, että syyn todennäköisyys – kausaalisuus – voidaan johtaa seurauksista. Syyn prioritodennäköisyys on parantamisessa ja tautien/vikojen tunnistamisessa keskeistä ja faktaa, ei ihmisten havaitsema posteritodennäköisyys.

Lopuksi vielä YouTube-video Bayesin säännöstä: 

Lähteet:

1. AIAG: Measuremet System Analysis, Fourth Edition, 2010
2. Eero E. Karjalainen: Kausaliteetti syy on ehto parannukselle – mitä se on? Artikkeli 2.4.2020
3. Judea Pearl, Dana Mackenzie: Miksi – Syyn ja seurauksen uusi tiede, 2018
4. Helsingin Sanomat, 7.5.2020, Vasta-aineiden testi voi väärän tuloksen
5. Helsingin Sanomat, 4.9.2020, Pikatesti voi paljastaa viruksen vartissa
6. Helsingin Sanomat, 11.9.2020, Muistio: Testaus maksaa 1,4 miljardia euroa vuodessa (STM)
7. https://thl.fi/documents/533963/5860112/Testauswebinaari_final_15.5.2020.pdf/ff78ae45-b4d8-e3a5-9861-7cc991b4fe65?t=1589553036389
8. Tanja Karjalainen ja Eero E. Karjalainen: Lean Six Sigma 2.0 ja Laatuteknologia, 2020