Juurisyyanalyysi (RCA) ja Shainin Systeemi™

Juurisyyanalyysi (RCA) ja Shainin Systeemi^™(SS)

Juurisyy (RC) on Suomessa suhteellisen uusi yleiskäsite, joka ilmestyi sanakirjaan 2010-luvulla. Laatutekniikassa juurisyy (Root Cause) esiintyi jo 1970 – 80 luvulta ja englanninkielessä 1800-luvun lopulta lähtien⁽¹⁾. 

Miksi tarvittiin uusi juurisyy käsite? Miksi ei käytetä ytimekästä sanaa SYY asian yhteydessä? 

Jokaiseen vähänkin monimutkaisempaan systeemiin, prosessiin, tuotteeseen ja palveluun liittyy lukuisia syitä, jopa tuhansia tai kymmeniätuhansia. Nämä syyt eivät ole vaikutukseltaan yhdenvertaisia. Syiden vaikutus tulokseen muodostuu Pareto-periaatteen ja varianssin summautumisen yhteisvaikutuksesta. Jos halutaan parantaa tai korjata systeemiä eli saada aikaan muutosta, vain muutamien syiden muuttaminen vaikuttaa haluttuun lopputulokseen merkittävästi. Asia on kuvattu ja perusteltu tarkemmin artikkelissa. On virhe sanoa, että kaikki vaikuttavat kaikkeen tai edes suurin osa vaikuttaa! Jos laite on viallinen, on virhe sanoa, että vaihtamalla osia, vika poistuu. Vika poistuu vain löytämällä viallinen osa ja vaihtamalla tai korjaamalla se, ”juurisyy”! Muiden osien vaihtaminen on turhaa työtä ja hukkaa.

Juurisyy on siis erityinen syy, joka poikkeaa ”tavanomaisesta” syyn käsitteestä. Se on kuin ohjauspyörä autossa. Tekemällä ohjaus tai muutos juuri tähän syyhyn, se saa aikaan voimakkaan suuntamuutoksen missä tahansa järjestelmässä – joko hyvään tai huonoon suuntaan. Olisipa kaikki ”ohjauspyörät” tiedossamme, mutta kun ei ole! 

Juurisyystä tai oikeastaan sen poikkeaman, muutoksen, aiheuttamasta vaikutuksesta käytetään myös käsitettä kausaliteetti (Artikkeli: Kausaliteetti-syy on ehto parannukselle – mitä se on?); juurisyyllä on kausaliteettivaikutus ulostuloon tulevaisuudessa, esimerkiksi tuotteiden ja palveluiden laatuun, virheisiin, vikoihin, hukkaan, tuottavuuteen ja kuten autossa, suunta muuttuu. Muilla syillä tätä vaikutusta ei ole. On myös huomattava, että jokaisella tuotteella, palvelulla tai prosessilla on samanaikaisesti lukuisia ulostuloja, joilla kullakin on omia ja yhteisiä juurisyyitä. Nämä juurisyyt saattavat olla täysin vastakkaisia toisilleen. Yhden syyn muuttaminen tai parantaminen heikentää toista – suo siellä, vetelä täällä. Esimerkkinä vaikkapa lääkkeiden pakkauksissa olevat pitkät luettelot mahdollisista sivuvaikutuksista.  

Kaiken tämän, siis juurisyyn olemassaolon takana, on kaksi vaikuttavaa oletusta systeemistä: 1. pareto-periaate ja 2. varianssin summautumisen teoria. Näihin kahteen oletukseen perustuu myös Shainin Systeemi (SS) ja itse asiassa kaikki RCA-analyysimenetelmät. 

Yleisesti meillä on kaksi selkeästi erilaista juurisyyn hakutilaa, jotka samalla jakavat menetelmät ja toimenpiteet parantamiseen ja korjaamiseen: 

1. Ihminen, tuote, palvelu, prosessi tai systeemi on stabiilissa tilanteessa, jossa tapahtuu vain satunnaisia muutoksia (ulostulomittareista nähtynä). 
   
2. Ihminen, tuote, palvelu, prosessi tai systeemi on ollut tai on epästabiilissa tilanteessa, jossa on tapahtunut tai tapahtuu merkittäviä, ei satunnaisia muutoksia (ulostulomittareista nähtynä).

Nämä kaksi eri aikatilaa voidaan erotella toisistaan eri tavoin. Laatutekniikassa erottelu tapahtuu yleensä ohjaus- ja valvontakorteilla ja kutsutaan SPC:ksi, Tilastolliseksi prosessin ohjaukseksi. Tilastotekniikassa käytetään erilaisia tilastollisia analyysejä ja hypoteesitestausta, joilla näytteiden osajoukot voidaan erotella toisistaan ja lääketieteessä kyse on diagnoosista – onko sairautta⁽²⁾ vai ei⁽¹⁾, onko sattumatapahtumasta erottuvaa aikamuutosta vai ei! Huomaa, että hyvä tai huono, ruma tai kaunis, viallinen tai ei (ihmisen mielipide), ei jaa hakutilaa vaan systeemin ominaisuus, stabiilisuus, muutoksen ajallisen ilmenemisen suuruus.

Ihmisen oletetaan terveenä ollessa olevan stabiilissa tilanteessa ja prosessit ja systeemit toimiessaan ”normaalisti” ovat myös stabiilissa tilassa. Tri Deming estimoi Out Of Crisis -kirjassa, että 94 % syistä on yhteisiä syitä (common causes) ja 6 % syistä on erityissyystä johtuvia (special cause). Lean Six Sigmassa ja Shainin systeemissä tämä stabiili tila ”murretaan”, joka mahdollistaa juurisyyn löytämisen ja parannuksen. Juurisyy on syy, joka muutettaessa vaikuttaa tutkittavaan ulostuloon.

Juurisyyanalyysit (RCA) 

Juurisyyanalyysit⁽²⁾ noudattavat edellä olevaa ”systeemi”jakoa:

1. Jos systeemin, prosessin, tuotteen, palvelun, ihmisen jossain ominaisuudessa (output) ei ole tapahtunut merkittävää muutosta ja halutaan tämän ominaisuuden muuttuvan vaikkapa laadun, tuottavuuden, hyötysuhteen, jonojen, hukan parantamiseksi, puhutaan parannuksesta (improvement). Jotta parannus, so. muutos saadaan aikaiseksi, on ensin selvitettävä kausaalinen syy tutkittavaan ominaisuuteen tai ominaisuuksiin, eli juurisyy(t) ja kohdistettava muutosvoima tämän tekijän, muuttujan, muuttamiseen. Tarvitaan siis juurisyyanalyysi, joka pystyy hakemaan ja analysoimaan ”yhteisen” piilossa olevan juurisyyn tai syyt (RCA).
   
2. Jos sen sijaan systeemin jossain ominaisuuksissa (output) on tapahtunut muutos, voi olla hyödyllistä selvittää tämän muutoksen aiheuttanut syy. Mitä todennäköisimmin tämä erityissyy on juurisyy. Uskomme nimittäin, että jokaisen muutoksen takana on syy tai syyt, ei sattumaa! Tarvitaan juurisyyanalyysi (RCA), joka pystyy hakemaan ja analysoimaan tämän erityisen syyn, joka on muuttumisen kautta ilmaissut ulostulolle olemassaolonsa luonteen ja jäljen. Tämä historiallista muutoksesta syytä hakeva tekniikka on huomattavasti helpompi analysoida kuin ei muutosta tilanteessa.

Juurisyyn löytämiseksi on kehitetty erilaisia hakualgoritmeja, laatumenetelmiä ja työkaluja. Joskus suurisyyn löytäminen tuhansien syiden joukosta on todella vaikeaa ja vaikka juurisyy löydettäisiin, oikean ratkaisun löytäminen voi olla vieläkin vaikeampi. COVID 19 virus löytyi helposti, mutta rokotteen kehittäminen oli vaikeaa.

Huom! Ihmisen tekemissä laitteissa on osa ”juurisyistä” tuotu käyttöliittymänä esille. Muuttamalla näitä koodeja tai säätimiä, esimerkiksi auton kosketusnäyttöä tai ohjauspyörää, kaasua, jarrua, ulostulo muuttuu. RCA-analyysissä haemme piilossa olevia juurisyitä. 

Lean Six Sigma ja Shainin menetelmä voi ”murtaa” stabiili systeemin tai prosessin, jossa ei ole tapahtunut muutosta, ja voit tehdä ”aidon” parannuksen. Muutama muukin harvemmin käytetty menetelmä löytyy kuten Juranin läpimurtostrategia, ”Diagnostic and Remedial Journeys Approach”⁽⁵⁾ ja Hoerlin ja Sneen⁽⁶⁾ ehdottamat ”Process Improvement and Problem Solving Strategies”. Myös Taguchi-menetelmä lasketaan joskus näihin systeemeihin, on-line ja off-line control, vaikka itse kirja ”Introduction to Quality Engineering – Design Quality into Products and Process”, 1986 käsittelee ensi sijassa laadun suunnittelua.

RCA 2, RCCA, Kepner Tregoe, 8D, A3, Apollo, TOC, 7 tools, EPS -analyysimenetelmät on tarkoitettu merkittävästi ulostuloon vaikuttavien toistuvasti tapahtuvien muutostilanteiden juurisyiden analysointiin ja näiden korjaamiseen. (Artikkeli: Juurisyyanalyysi vai pinnallinen syyanalyysi?) Tämän muutostapahtuman on todennäköisesti peräisin prosessin kausaalista juurisyystä, erityissyystä (special cause). Menetelmissä korostuu prosessi, josta yritetään hakea juurisyytä erilaisten algoritmien ja kysymyslistojen avulla. 

Logiikkapuu (RCA 1) (Artikkeli: Pimeän näytön juurisyyanalyysi), Tap Root, erilaiset onnettomuus ja tapaturmatutkimukset tarkastelevat yksittäistä ei-toivottua tapahtumaa, onnettomuutta, vahinkoa, reklamaatiota, hoitovirhettä, rikosta, jonka juurisyy pitää selvittää.⁽⁴⁾ Nämä menetelmät kattavat läheisten syiden strategian⁽²⁾, jossa yksittäisen tapahtuman kausaalisyyt, juurisyyt yritetään selvittää.

Kaikki menetelmät perustuvat yhteen tai useampaan hakustrategiaan, joita käsittelin artikkelissa Juurisyyn löytämisen strategioita⁽²⁾. Valitettavan usein lankeamme kuitenkin pinnallisten syiden analyysiansaan⁽³⁾. Ansa virittyy ja laukeaa, kun emme testaa ja tutki, muuttuuko ulostulo, kun muutamme olettamaamme juurisyytä.

Tässä artikkelissa käsitellään yhtä tunnetuimmista satunnaissyyperusteisten syiden RCA-menetelmää ns. Shainin Systeemiä (SS).  Menetelmä on lähes rinnakkainen Lean Six Sigma -menetelmän kanssa, mutta lähestymistapa on osin erilainen. Molemmissa on lainattu menetelmiä toinen toiseltaan. 

Sisältö:

1. Shainin Systeemin luoja, Dorian Shainin
2. Shainin systeemin peruskonsepti
3. Itsenäisten syiden yhdistelmä
4. Shainin systeemin ohjaavat periaatteet
5. Vaihtelun hallitsevat syyt (Red x) ja progressiivinen haku – poissulkeva ”oksa ja karsi ” strategian sovellutus.
6. Ongelmanratkaisun algoritmi
6.1 Diagnostisen matkan algoritmi
6.2. Korjaavan matkan algoritmi
7.  Shainin systeemin keskeiset työkalut
7.1. Luo tehokas mittaussysteemi
7.2. Vihjeiden generointi
7.3. Punaisen X:n eristäminen
7.4. Realististen toleranssien määrittäminen
7.5. Tilastollisen prosessin ohjauksen toteuttaminen
8. Shainin ja Six Sigma menetelmät ja niiden yhtenevyydet ja erot 
9. Yhteenveto ja johtopäätökset
10. Shainin Systeemin käyttöesimerkkejä
11. Viitteet

SHAINININ SYSTEEMI (SS)

1. Shainin Systeemin luoja Dorian Shainin

”Great” Dorian” Shainin⁽⁷⁾ kuuluu laatuyhteisön suuriin nimiin Shewhartin, Demingin, Juranin, Tukeyn, Weibullin ja Taguchin rinnalla.  

Minulla on ollut suuri kunnia tavata Dorian muutamia kertoja 1990-luvulla, kun osallistuin hänen pitämäänsä Shainin seminaariin ja keskustellessani useasti ASQ World Conferensseissa hänen kanssaan. Hauska, originelli ”veikko” (n. 160 cm) villasukissaan! 

Hän oli syvästi kunnioitettu ja lukuisilla arvonimillä palkittu (Honorary Member of ASQ). Hänet tunnettiin vaikeiden teollisten ongelmien ratkaisijana ja oli osaltaan vaikuttamassa Six Sigman syntyyn Motorolalla 1980-luvulla. Hänet palkittiin vuonna 1989 Malcom Baldrige Quality Award-palkinnolla yhdessä Motorolan kanssa. Hänen kunniakseen jaetaan vuosittain harvinainen elämäntyöpalkinto, Dorian Shainin Medal. 

Dorian Shainin kehitti Shainin ”Red X” (Punainen X) -metodologian 1950-1990 -luvuilla ja lukuisia tähän liittyviä keskeisiä analyysi- ja koemenetelmiä (taulukko 1) ja viimeisimpänä analyysitekniikan, Shainin System™, lähes samaan aikaan, kun Six Sigma kehittyi tri Mikel Harryn toimesta.

2. Shainin Systeemin peruskonsepti 

Shainin Systeemin (SS) peruskonsepti voidaan tiivistää seitsemään perusväittämään (9):

1. Kaikki työ tapahtuu toisiinsa liittyvien prosessien järjestelmässä.
2. Kaikissa prosesseissa on vaihtelua
3. Vaihtelun ymmärtäminen ja vähentäminen ovat avaimia menestykseen
4. Todellisessa maailmassa mitään ei tapahdu ilman syytä
5. Aina on olemassa Punainen X (Red X = juurisyy = hallitseva syy = kausaalisyy)
6. Punaisen X:n löytäminen ja hallinta on ainoa tapa vähentää vaihtelua ja tehdä merkittävä parannus
7. Paras tapa löytää Punainen X on suorittaa progressiivinen hauku ”puhumalla osille” so. keräämällä aktiivisesti osien avulla vihjeitä ja suuntaamalla näiden vihjeiden avulla juurisyyn hakua. 

Nykyään Shainin Punainen X -metodologia koostuu noin 30-40 tekniikasta ja työkalusta – tunnetuista ja äskettäin kehitetyistä – jotka luovat kattavan vaiheittaisen järjestelmän vaikeiden ongelmien ratkaisemiseen ja prosessien parantamiseen. Dorian Shainin työtä jatkaa pojat Richard ja Peter Shainin https://shainin.com .

Shaininin ongelmanratkaisun tiekartta on nimeltään FACTUAL (Focus, Approach, Converge, Test, Understand, Apply, Leverage) on esitetty taulukossa.

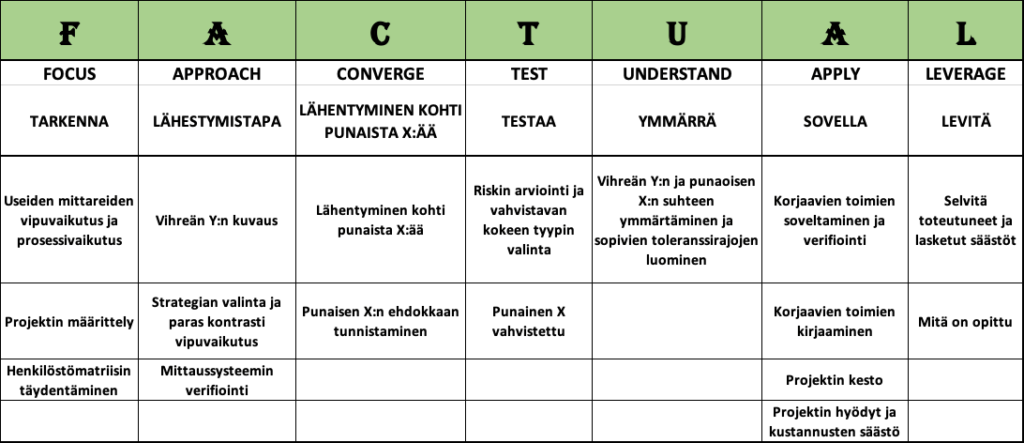
Shainin systeemi perustuu ”oksa ja karsi” strategiaa⁽²⁾, jossa lähennytään vaihe vaiheelta kohti Punaista X:ää. Mitä se tarkoittaa? On ehdottoman välttämätöntä ymmärtää prosessin tulos, output – vihreä Y. Mitään ongelmaa ei voida Shaininin mukaan ratkaista ilman tietoa ulostulosta, outputista ja siihen liittyvistä prosesseista, vian oireista sekä hyvien ja huonojen osien eroista. 

Tämä varmistetaan menetelmällä, jota kuvataan ”osien kanssa puhumiseksi”. Tämä tarkoittaa joukkoa tekniikoita, joita käytetään ongelman lähentymiseen (converge), kuten epäiltyjen eliminointi, hyvien ja huonojen osien vertailu, äärimmäisyyksien löytäminen. 

Matemaattisesti ilmaistuna on ymmärrettävä suhde ΔY = f(ΔX). Avainero Shainin Punainen X -strategian (FACTUAL) ja Six Sigma -metodologian (DMAIC) välillä on vaiheittainen lähestymistapa, jolla haetaan mahdollisia vihjeitä Punaisesta X:stä. Jokaisen karsintavaiheen jälkeen suuntaa ja työkalua, strategiaa, harkitaan, kuva 7.

Ongelmanratkaisija kehittää SS:ssä strategian, joka perustuu ongelman fysiikkaan ja ”parhaimmista parhaimpien” (BOB, Best of the Best) ja ”huonoimmista huonoimpien” (WOW, Worst of the Worst) -osien vertailuun ja eroihin. 

Six Sigmassa haku perustuu tilastollisiin jakaumapoikkeamiin satunnaisesta jakaumasta, yleensä normaalijakauma. Työkalut seuraavat järjestyksessä toinen toistaan. Vaikka prosessi on stabiili, voi prosessissa olla sisäisesti epästabiilisuutta, joka saattaa Lean Six Sigmassa johtaa juurisyyn jäljille. Tarvitaan kuitenkin vahvoja ja laajoja kokeita (DoE) epäiltyjen tekijöiden lopulliseksi poissulkemiseksi ja juurisyyn paljastamiseksi. 

Shainin Punainen X -metodologian avainideana on Punainen X -paradigma⁽¹¹⁾. Tämä paradigma syntyy Pareto-periaatteen soveltamisesta vaihtelun syihin (input sigma, kuva 2a) ja varianssin summautumisesta, kun syyt ”tuodaan” ulostuloon (output sigma, kuva 2b).

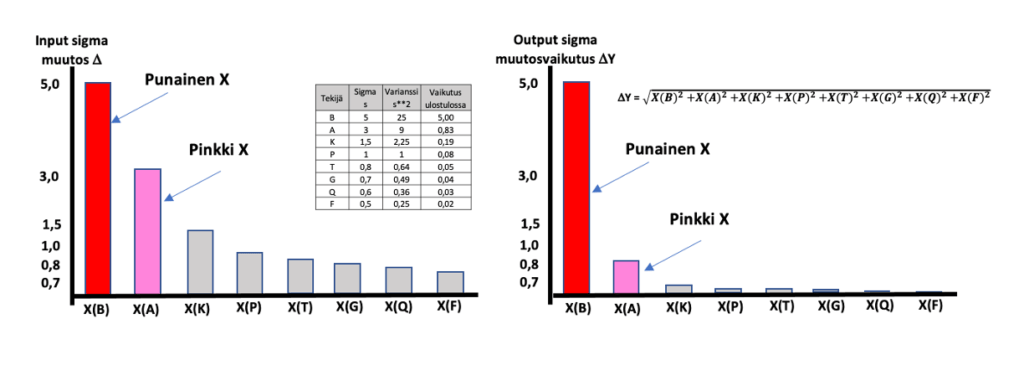
Pareto 80/20 – periaatetta soveltamalla saat X:n (prosessin inputtien) panoksen muunnettua varianssien nelijöiden summan neliöjuurella ∆Y:ään (outputin lisäys), kuten kuvassa 2 näkyy. Saattaa olla tapauksia, joissa tunnistetaan jopa kolme syytä – Punainen X, Vaalean punainen X, Haalean vaalean punainen X (Red X, Pink X, Pale Pink X ) – jotka ovat yleensä vuorovaikutuksessa Punaisen X:n (Red X) kanssa.

3. Itsenäisten syiden yhdistelmät

Punaisen X:n (Red X) täyden merkityksen ymmärtämiseksi on hyödyllistä tarkastella vielä tapaa, jolla riippumattomat jakaumat yhdistyvät. 

Kun riippumattomat jakaumat (Y=keskiarvo, s=keskihajonta, s²=varianssi) yhdistetään tai vähennetään toisistaan, tuloksena olevan jakauman keskiarvo on lähdejakaumien keskiarvojen summa ja/tai erotus (Y= Y₁ ± Y₂ ± …Y_n). Tuloksena olevan jakauman varianssi (s²) on lähdejakaumien riippumattomien varianssien summa (s²=s₁² + s₂²+ …s_n²). Riippumattomat keskihajonnat (s) eivät koskaan laskeudu yhteen summaksi ja/tai erotukseksi kuten lähdejakaumien keskiarvot (ei näin s≠s₁±s₂± …s_n) vaan vain summaksi.  

Yhdistetyn jakauman keskihajonta on aina lähdejakaumien keskihajontojen neliöiden summan neliöjuuri .  Keskihajonnan eli standardipoikkeaman s toinen potenssi on varianssi = s². Tämä riippumattomien varianssien summautumis-sääntö pätee riippumatta lähdejakaumien muodosta. 

Keskihajonnan neliöiden summan neliöjuuri lisää Punaisen X:n vaikutusta entisestään (kuva 2b). Ajatellaan, että jos Punainen X aiheuttaa 5 yksikön vaihtelua ja pienempi syy on 2 yksikköä, suhteellinen vaikutus lähdössä (output) on 25:4, ei 5:2. Ilmiö näkyy selvästi kuvassa⁽²⁾. Parannusta hallitsee yleensä vain yksi tai kaksi muuttujaa, harvoin kolme. (Katso artikkelin 2 kuvaa 3). Muiden tekijöiden muuttaminen ei vaikuta merkittävästi haluttua lopputulosta, mutta voi aiheuttaa voimakkaan ei toivotun sivuvaikutuksen. Tämä on seurausta kahdesta päällekkäisestä ilmiöstä: Pareto-periaate esiintyy syiden tasolla ja varianssin summautuminen tapahtuu ulostulossa.

Voimme tehdä nyt useita johtopäätöksiä systeemi- ja prosessiongelmien ratkaisemisesta ja laadun parantamisesta:

1. Jokaisella prosessilla on aina yksi vaihtelun juurisyy, joka on suurempi kuin mikään muu (Punainen X). Tämä voi olla yksittäinen muuttuja tai synergistinen interaktiivinen vaikutus useista muuttujista yhdessä Punaisen X:n kanssa. Harvoin vaikuttavia tekijöitä on kaksi tai kolme.
2. Koska muuttujien riippumattomat keskihajonnat yhdistyvät neliösumman neliöjuureksi, ainoa tapa tehdä merkittäviä parannuksia prosessin vaihtelun vähentämisessä on löytää Punainen X ja hallita sitä. Punainen X on juurisyy. Näin ollen ei ole olemassa pienten parannusten polkua, jossa ”pienetkin” teot mihin tahansa syihin vaikuttavat yhdessä merkittävästi. Fysikaalisesti ja matemaattisesti mahdoton tilanne! Juran kutsui tilannetta ”Vital few, trivial many!”  
3. Ei ole olemassa sellaista asiaa kuin satunnainen vaihtelu (random variation), mutta on olemassa satunnaiset, yhteiset syyt (chance, common causes). Jokaiselle ulostulolle Y on useita syytekijöitä X, jotka vaikuttavat vaihteluun. Riittävällä resurssilla, mukaan lukien tehokkaat mittausjärjestelmät ja aika, voisimme löytää kaikki nämä X:t, mutta vain yksi tai kaksi syyn muutosta vaikuttaa merkittävästi. 

P.S. Käsittelen syykäsitteitä artikkelissa Jatkuvasta tarkastuksesta ja korjauksesta jatkuvaan parantamiseen tai sitten ei?. Tri Walter A. Shewhart määritteli vuonna 1931 syyluokat ja käytti syistä termejä assignable cause, chance causes – ositettavissa oleva syy, satunnaissyyt. Tri W Edwards Deming nimesi vuonna 1983 nämä syyt uusilla nimillä special cause, common causes – erityissyy, yhteiset syyt. Näistä syyluokista on Suomessa käytetty yleensä yhdistelmää erityissyy, satunnaissyyt. Wikipediasta lisää https://en.wikipedia.org/wiki/Common_cause_and_special_cause_(statistics)

Huom! SPC:llä jaetaan vaihtelu ekonomisesti (talouden perusteella) erityissyihin (special, assignable cause) ja yhteisiin, satunnaissyihin syihin (common, chance causes). Erityissyyt, juurisyyt tulee ja pitää selvittää ja korjata, jotta stabiilisuutta voi ylläpitää. Yhteisten, satunnaissyiden tutkiminen veisi liikaa resursseja. Lean Six Sigmalla ja Shainin Systeemillä yhteisten syiden tutkiminen kuitenkin onnistuu taloudellisesti, jos ongelman tai parannuksen tuotto on riittävä eli kattaa vähintään kulut. Siksi yleensä vaaditaan ennen projektin alkua ”kannattavuuslaskelma” potentista ja asetetaan tavoite. 

4. Shainin Systeemin (SS) ohjaavat periaatteet

SS:n taustalla olevat periaatteet voidaan jakaa kahteen ryhmään⁽¹²⁾. 

1. Ensimmäinen ryhmä muodostuu ajatuksesta, että vaihtelulla on hallitsevia syitä, juurisyitä, joita SS:ssä kutsutaan Punainen X, Vaalean punainen X, Haalean vaalean punainen X (Red X, Pink X ja Pale Pink X). Tämä periaate esiintyy ensimmäisen kerran Juranin ja Grynanin teoksessa (13), mutta Shainin hyödyntää tätä käsitettä täysin. 
2. Toinen ryhmä periaatteita on upotettu algoritmiin, Shainin Systeemiin, joka näkyy kuvassa 3 vasemmalla ja oikealla keskeiset työkalut.

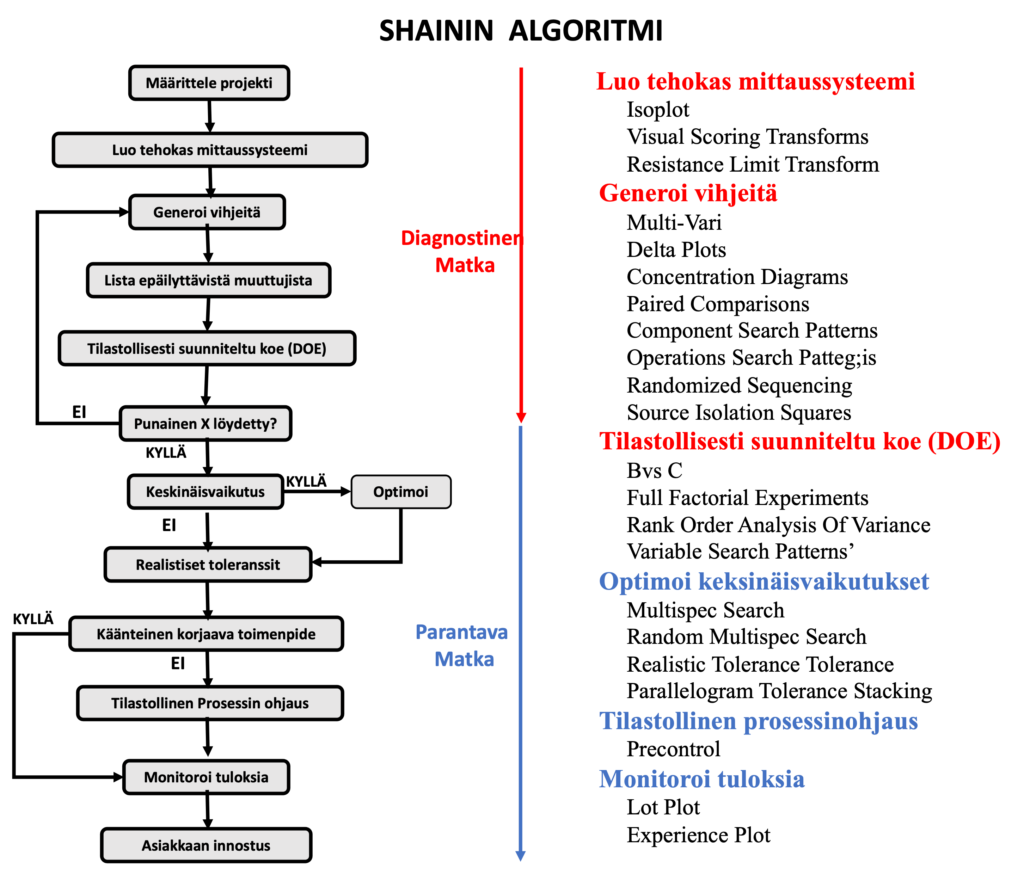
SS jakaa parannusprosessin kahteen osaan: diagnostinen matka ja parantava matka (Diagnostic Journey ja Remedial Journey), kuten Juran. Katso artikkeli: Juurisyyn löytämisen strategioita).

5. Vaihtelun hallitsevat syyt ja progressiivin haku – poissulkeva ”oksa ja karsi” -strategian sovellutus

SS:n perusperiaate on, että kaikille ongelmille on hallitseva juurisyy. Prosessin ulostulon vaihtelu määrittelee ongelman, ei siis ulostulon suuruus tai pienuus. SS:ssä hallitseva syy on nimeltään Punainen X. Hallitsevan syyn korostaminen on perusteltua, koska Punaisen X:n vaikutus kasvaa, koska useiden inputtien yhteisvaikutus lasketaan neliösumman neliöjuurena⁽¹⁴⁾. Suora seuraus tästä on, että emme voi merkittävästi pienentää outputin keskihajontaa tunnistamalla ja poistamalla tai ohjaamalla muiden yksittäisten syiden vaikutusta. Pelkän vaihtelun keskiarvon muuttaminen ei yleensä johda systeemin parannukseen. Keskiarvolla voidaan säätää. Keskiarvon säätö vaatii ± mahdollisuuden! Säätötulosta ei yleensä kutsuta parannukseksi, vaikka voi olla parempi!

SS käyttää eliminointiprosessia, poissulkuprosessia⁽¹⁵⁾, jota kutsutaan progressiiviseksi hauksi. Tällä tunnistetaan hallitsevia syitä. Progressiivinen haku toimii paljolti strategiapelin ”20 kysymystä” tapaan, jossa yritämme löytää oikean vastauksen käyttämällä sarjaa kyllä/ei-kysymyksiä. Kysymykset jakavat hakutilan pienemmille ja pienille alueille. Tätä käsiteltiin artikkelissa⁽²⁾ kohdassa 4.1. Sekvenssirakenne ja puolittaminen.

Eliminointiprosessin toteuttamiseksi SS käyttää vaihtelun syiden perheitä, joissa kussakin voi olla kymmeniä, jopa satoja yksittäisiä syitä. Vaihteluperhe on ryhmä vaihtelevia prosessi-inputteja, jotka toimivat samassa paikassa tai samassa aikavälissä. Perheitä ovat esimerkiksi osan sisällä olevat syyt, osasta osaan (peräkkäinen) olevat syyt, tunnista tuntiin syyt, päivästä toiseen syyt, koneesta koneeseen olevat syyt. Missä tahansa etsinnän vaiheessa ajatuksena on jakaa mahdolliset hallitsevat syyt toisensa poissulkeviin perheisiin ja tehdä sitten tutkimus, joka eliminoi kaikki muut perheet paitsi yhtä, joka on hallitseva perhe, jonka kotona on hallitseva syyn. Tämän menetelmän keksi Leonard Seder vuonna 1950⁽²¹⁾. Leonard löysi aukon Walter Shewhartin luomasta laatuteoriasta (SPC).

Progressiivinen haku toimii oletuksella, että hallitsevia syitä on vain yksi tai kaksi. Jos voimme kohdistaa suurimman osan havaitusta vaihtelusta yhdelle perheelle, voimme poistaa kaikkien muiden perheiden aiheuttamat vaihtelupanokset vaikuttamatta hallitsevan syyn perheeseen. Oletetaan esimerkiksi, että monimuuttujatutkimuksessa (katso seuraava osio) havaitsemme, että vaihtelu osasta osaan on paljon suurempi kuin vaihtelu ajasta aikaan. Siten kaikki vaihtelevat inputit, jotka muuttuvat pidemmällä aikavälillä, kuten raaka-aine-erien ominaisuudet, voidaan eliminoida hallitsevina syinä.

Toinen seuraus hallitsevan syyn oletuksen on, että hallitsevasta syystä saadaan paljon tietoa vertaamalla toisiinsa yksiköitä, tuotteita, joissa esiintyy ääriarvoja (output). Siis tutkimalla eroja. Tämän ”vipuvaikutuksen” käyttö on ainutlaatuista SS:lle⁽¹⁶⁾. SS:ssä käytetään vertailuun ”parhaimmasta parhaimpia” (BOB= Best of the Best) ja ”huonoimmista huonoimpia” (WOW = Worst of the Worst) -yksiköitä/osia. Hallitsevan syyn arvojen (tuotteiden, osien) tulee olla olennaisesti erilaisia näissä kahdessa ryhmässä, jotta ero on tunnistettavissa. Ne eivät saa kuitenkaan olla viallisia tai erityissyitä. Vipuvaikutuksen etu on se, että voimme eliminoida syyperheitä käyttämällä tutkimuksissa pieniä näytteitä äärimmäisistä yksiköistä. Vipuvaikutuksen ideaa käytetään erityisesti monissa SS-työkaluissa, mukaan lukien komponenttihaku, muuttujahaku ja ryhmävertailu (Component Search, Variable Search, Grup Compairson), joita käsittelen myöhemmin tässä artikkelissa. 

SS välttelee aivoriihiä ja syy-seurauskaavioita tutkiessaan mahdollisia syitä. Syy-seuraus-analyysi, kun kaikki tai suuri määrä mahdollisuuksia on tunnistettu, pakottaa tarkastelemaan useita mahdollisia hallitsevia syitä yksi kerrallaan tai jossain yhdistelmässä. Progressiivisen haun ja huolellisesti suunniteltujen havaintotutkimusten avulla voidaan sulkea pois suurperheet ilman, että koskaan tunnistamme perheen muodostavia yksilöitä. Dorian Shainin⁽¹⁷⁾ toteaa: ”Vakavien ongelmien ratkaisussa ei ole sijaa subjektiivisille menetelmille, kuten aivoriihille tai kalanruotokaavioille.”

Progressiivisen haun onnistuminen riippuu kyvystä yhdistää prosessitutkimusten tuottamaa empiiristä tietoa ja suunnittelu- ja prosessitietoa. Prosessin tiedon tarve korostuu koko SS-metodologiassa. Tutkijalla tai ryhmällä on oltava syvä ymmärrys prosessista, jonka avulla voidaan rakentaa sopivia perheitä, suunnitella tutkimuksia ja tunnistaa tietty perhe hallitsevan syyn kodiksi. Prosessiosaaminen on myös olennaista määritettäessä asianmukaista tuotetta, prosessia tai ohjaussuunnitelmaa koskevaa muutosta, joka vähentää tai eliminoi tunnistetun hallitsevan syyn vaikutusta. 

SS:ssä ei ole tarkkaa erittelyä ja vaatimusta siitä, ovatko hallitsevat tai muut syyt yhteisiä vai erityisiä (common, special) kuten SPC:ssä. Hakustrategia on suunniteltu etsimään yhtä tai kahta syytä, joilla on suuri vaikutus ulostulovarianssiin. 

Vaihtelun vähentämisongelmissa (suorituskyvyn parantamisessa) variaatioperheiden ja eliminointimenetelmän käyttö on tehokkaampi tapa jakaa syyt hallitseviin ja ei-hallitseviin syihin kuin klassinen Statistical Process Control (SPC) -jako yhteisiin ja erityisiin syihin. 

Progressiivisen haun käyttö ei ole vaivatonta. Voi olla vaikeaa tunnistaa hallitsevaa syytä, joka on keskinäisvaikutus erilaisten inputtien välillä eri perheissä, jos ei tunne prosessia ja sen fysiikkaa/kemiaa. Six Sigmassa tämä prosessiosaamisen ja fysiikan tuntemuksen vaatimus on alhaisempi.

6. Ongelmanratkaisun algoritmi

Ongelmanratkaisun SS-vaiheet on esitetty kuvassa 3. Huomaa, että algoritmi on määritelty yhdelle projektille, mutta se on samalla suunniteltu sopimaan laajempaan projektinvalinta- ja hallintaprosessiin. 

Algoritmi on jaettu kahteen osaan, diagnostiseen ja parantavaan matkaan. Terminologia tulee Juranilta ja Grynalta⁽⁵⁾. 

• Diagnostisella matkalla ongelma määritellään, mittausjärjestelmä arvioidaan ja hallitsevaa/dominantia vaihtelua aiheuttava syy tunnistetaan ja varmistetaan. 
• Parantavalla matkalla hallitsevan syyn vauhteluvaikutus eliminoidaan tai vähennetään muuttamalla tuotesuunnittelua, prosessia tai ohjaussuunnitelmaa.

6.1. Diagnostisen matkan algoritmi

6.1.1. Algoritmin ensimmäisen vaiheen tarkoituksena on kvantifioida valitun ongelman suuruus. Ongelma voi olla ominaisuus, osakokonaisuus, vika tai tapahtuma (feature, property, defect, event), joilla kullakin on oma lähenemis-strategia. Tätä varten seurataan prosessin/tuotteen outputtia sopivalla otanta-menetelmällä (usein monimuuttuja-suunnitelmalla, multivari plan) riittävän pitkän ajan, jotta näemme kaikkien suurien vaihtelua aiheuttavien syiden vaikutuksen ja erityisesti hallitsevan syyn muutoksen vaikutuksen. Prosessin vaihtelu esitetään käyttämällä histogrammia tai numeerista yhteenvetoa. SS-terminologiassa tätä perustason histogrammia kutsutaan Vihreän Y-jakaumaksi⁽¹⁶⁾.

Perusjakaumaa käytetään ongelman suuruuden määrittämiseen ja tavoitteen asettamiseen. Nykytilan ja tavoitteen välinen ero muodostaa prosessin parannuspotentiaalin, ja mahdollisten ehdotettujen parannustoimenpiteiden suuruuden arvioimisen. Perusjakaumaa käytetään myös varmentamaan, että hallitseva syy esiintyy täydellä vaikutuksella jokaisessa progressiivisen haun tutkimuksessa. Tätä kutsutaan täyden vaihtelun alueeksi (full range of variation). SS:n epätavallinen piirre on selkeä yhteys hallitsevan syyn etsimisen ja perusjakauman välillä verrattuna muihin juurisyymenetelmiin.

6.1.2. Algoritmin toinen vaihe (katso kuva 3) sisältää kvantifioinnin ja tehokkaan mittausjärjestelmän perustamisen. Ilman hyvää mittausjärjestelmää prosessin analysoiminen ja parantaminen on vaikeaa. Itse mittausjärjestelmä voi olla ongelman hallitseva syy. SS-lähestymistavassa on Six Sigman lailla erillinen vaihe, joka on omistettu mittausjärjestelmän tarkistamiselle. Se auttaa varmistamaan, että tätä olennaista tehtävää ei laiminlyödä. SS painottaa mittausjärjestelmän tarkistamista prosessin outputtia vasten ja vertaamaan erottelukykyä, diskriminaatiota.

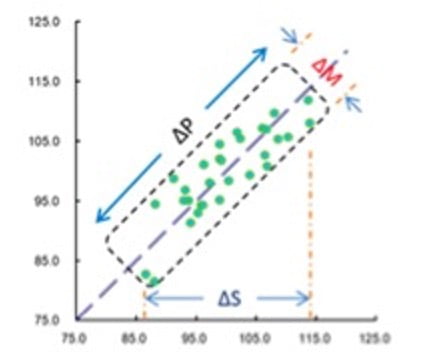
Kuvassa esimerkki nokka-akselin kiilauran tiukkuutta käsittelevästä ratkaisupuusta, jossa aluksi on tarkastettu mittaussysteemi ∆M ja tuotevaihtelu ∆P ja todettu, että diskriminaatiosuhde ∆P/∆M > 6 (19,2).  Mittauksessa vaadittava diskriminaatio eli erottelu määritetään ISOPLOT- menetelmällä. Kun mittaus (∆M) on eliminoitu, siirrytään seuraavaan hakuvaiheeseen. Lopulta on ratkaisupuussa vaiheittain syitä karsimalla päädytty juurisyynä leikkausleveyteen (cutter with)⁽²³⁾. 

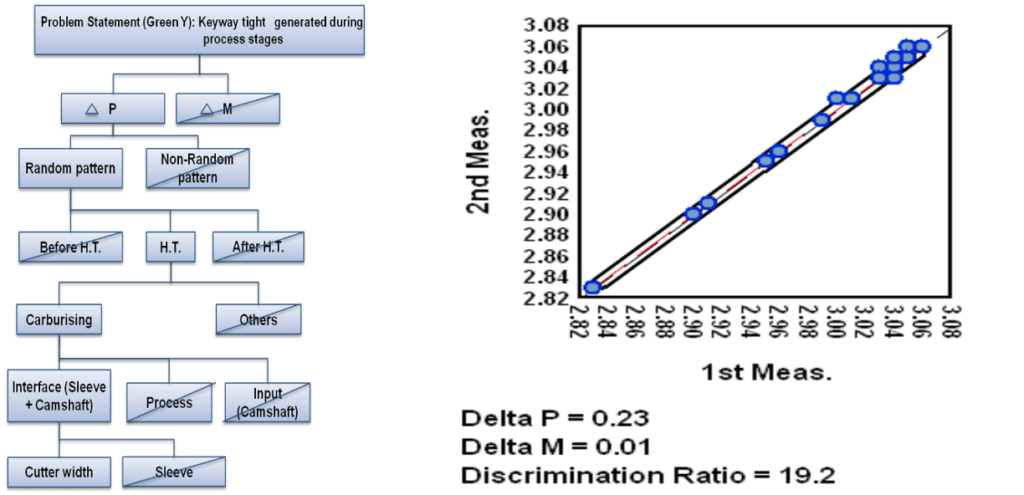
6.1.3. Algoritmin kolmannen vaiheen tavoitteena on tuottaa vihjeitä (clues) hallitsevista syistä. Tämä toteutetaan progressiivisella haulla. Tässä vaiheessa toinen keskeinen painotus SS:ssä on ”puhua osille”⁽¹⁸⁾. SS:ssä käytetään haussa paljon havainnointiin perustuvia suunnitelmia, kuten monimuuttujatutkimuksia (multivari investigations), kerrostuneisuutta (stratification), ryhmävertailua (grup comparison) ja hajontakuvioita ja korrelaatioitakuvioita (scattern plots, correlations plots). Suositellut koesuunnitelmat, kuten kokoonpanon komponenttien vaihtaminen (component swapping) tehdään off-line-tilassa, jolloin vältetään tuotannon häiriintyminen. Havaintosuunnitelmien sarja- ja perättäiskäyttö (sequental) on tehty ensisijaiseksi ja sitä korostetaan SS:ssä hallitsevan syyn etsinnässä. Tässä Shainin systeemi poikkeaa Six Sigmasta.

6.1.4. Algoritmin neljännen ja viidennen vaiheen tarkoituksena on vahvistaa hallitsevan syyn identifiointia. Progressiivisen etsinnän lopputulos voi olla yksittäinen syy tai lyhyt luettelo epäillyistä hallitsevista syistä. SS:ssä hallitsevat syyt varmistetaan muodollisen kokeen (DOE) avulla. Tällä halutaan estää mahdollinen sekoittuminen (confounding) ja väärät korrelaatiot (pienen otoskoon vuoksi). 

Epäillyt hallitsevat syyt ovat tekijöitä, jotka on pidettävä kokeessa kiinteinä tasoina. SS käyttää kahden tason mallia, joiden tasot on asetettu epäiltyjen syiden normaalien vaihtelualueiden päihin. Hallitsevan syyn tasojen muuttaminen kokeessa pitäisi tuottaa koko outputvaihtelualue, joka määritettiin algoritmin ensimmäisessä vaiheessa. Täydellisiä tekijäsuunnitelmia (full factorial design) suositaan, jotta epäiltyjen välinen keskinäisvaikutus voidaan tunnistaa. Yhdelle epäillylle tekijälle SS suosittelee kuuden ajon koetta, jota joskus kutsutaan B vs. C (Better vs Current), jossa on kolme toistoa kullekin tasolle satunnaisessa järjestyksessä.

Täystekijä (full factorial) varmennuskoe on mahdollinen, koska epäiltyjen luettelo on lyhyt. Lisäksi, koska tarkoitus on selvä, ei ole juurikaan mahdollista sekoittaa hallitsevan syyn tarkistamista ja parannustoimenpiteiden etsimistä. Toisin sanoen tässä vaiheessa normaalisti kiinteitä inputteja ei muuteta kokeen sisällä. 

6.2. Parantavan matkan algoritmi

Oletamme, että hallitseva syy on tunnistettu ja vahvistettu. 

6.2.1. Ensimmäinen askel parannusmatkalla koskee yksittäisen hallitsevan syyn erikoistapausta, joka on kahden vaihtelevan inputin välinen keskinäisvaikutus (interaction). Toisin sanoen outputin vaihtelun pääkomponentti, jota merkitään Y:llä, voidaan selittää kahden muuttujan tulolla, jotka on merkitty x₁:llä ja x₂:lla ja tasoilla 1 ja 2. Keskinäisvaikutuksen olemassaolo viittaa epälineaariseen suhteeseen y =f (x₁, x₂) + jäännös, jossa jäännösvaihtelu on suhteellisen pieni, koska x₁ ja x₂ yhdessä ovat hallitseva syy. On ehkä mahdollista hyödyntää suhdetta prosessin herkkyyden vähentämiseksi muuttamalla x₁:n, x₂:n tai molempien asetuspisteitä.

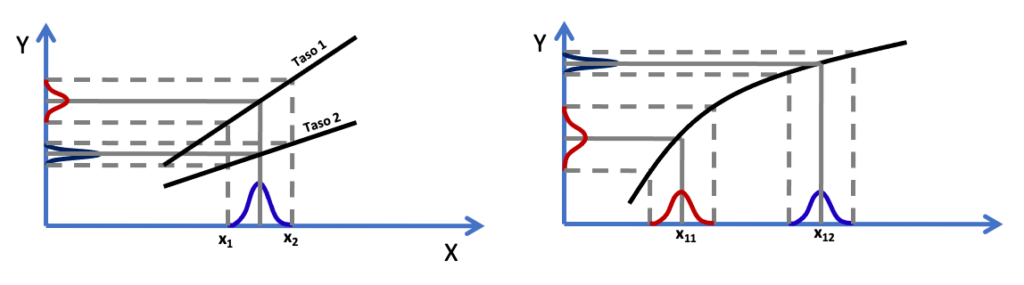
Voimme tutkia tätä mahdollisuutta sarjalla pieniä kokeita kahdella tekijällä x₁ ja x₂. Tämä strategia voi olla tehokas tai ei. Se on parametrisuunnittelun erityinen sovellus (Taguchilta peräisin), jossa kokeelliset tekijät rajoittuvat inputtien asetuspisteisiin, jotka muodostavat hallitsevan syyn. Taguchi kuitenkin suosii parametrien epälineaaristen ominaisuuksien käyttöä mielummin kuin keskinäisvaikutuksia. Epälineaarisuus on robustimpi. SS:n selkeä heikkous Six Sigmaan on, että siinä ei ole tilastollista optimointia (Minitab Optimizer), joka helpottaa epälineaarista optimiasetuksen hakua. SS:n etu toisaalta on, että parantavassa matkassa käsittelemme vain hallitsevia syitä. Resursseja ei tuhlata merkityksettömien häiriötekijöiden tutkimiseen.

6.2.2. Algoritmin toisen askeleen tavoitteena on määritellä realistiset spesifikaatiot (toleranssit) hallitsevaa syytä vastaavalle inputille. Nämä X:n spesifikaatiot voidaan löytää ulostulon (outputin) toleranssin perusteella määrittämällä inputin ja hallitsevan syyn välinen suhde. Tämä määritetään kokeellisesti 30 mittaparin (y, x) avulla ja laaditaan toleranssisuunnikas (Tolerance Parallelogramm Plot).⁽¹⁵⁾. 

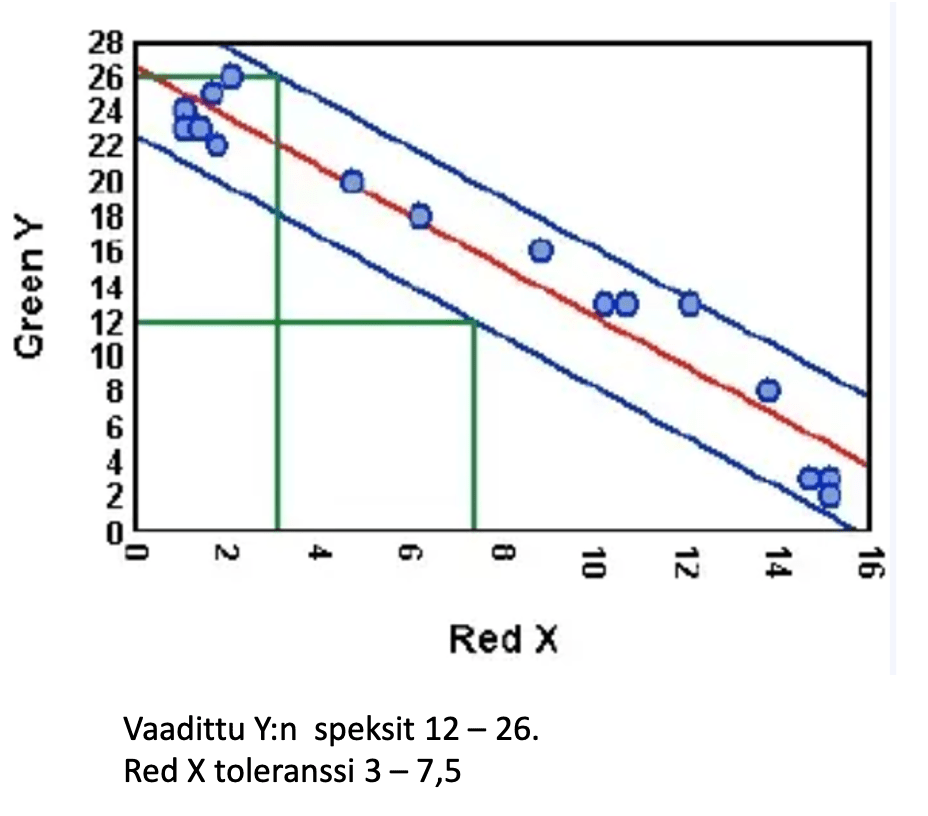
6.2.3. Algoritmin kolmannessa vaiheessa tehdään parantavia toimenpiteitä, jotta syyn vaihtelu voidaan poistaa. Jos tämä ei ole mahdollista, niin algoritmi ehdottaa prosessin ohjausta (Process Control). SS-terminologiassa tämä tarkoittaa esiohjausta (Precontrol), ei Shewhartin SPC-ohjauskortteja.

Esiohjaus on takaisinkytketty ohjausjärjestelmä, jota sovelletaan hallitsevaan syyhyn niin, että pidetään sen arvo edellisessä vaiheessa johdetuissa speksirajoissa. Esiohjaus eli precontrol on takaisinkytkentäsäädin, joka on suunniteltu osaksi säätöjärjestelmää, ja siksi sitä tulee verrata muihin takaisinkytkentäsäätimiin. Feedback ohjaus on tehokasta vain, jos hallitseva syy on luonteeltaan rakenteellisen vaihtelun omaava⁽¹⁹⁾. Toisin sanoen hallitsevan syyn tulee vaihdella siten, että voimme ennustaa tulevaisuuden nykyisten ja menneiden arvojen perusteella, ja näin on mahdollista tehdä oikeita muutoksia tarpeen mukaan. 

6.2.4. ja 6.2.5. Algoritmin kaksi viimeistä vaihetta eivät vaadi enempää keskustelua.

Yhteenveto: algoritmi on erittäin vahva diagnostisessa matkassa, mutta heikohko ja epätäydellinen parantavassa matkassa osin ehkä siksi, että parannus on usein itsestään selvä, kun juurisyy on löydetty ja vahvistettu. 

Suunniteltujen kokeiden (design of experiments, DOE) käyttö olemassa oleviin prosesseihin on yleistä kaikissa tunnetuissa (teollisissa) ongelmanratkaisu-menetelmissä. Ilman koetta on lähes mahdotonta parantaa toimintaa, koska juurisyy ”ilmaisee” itsensä vain muutoksessa. Kaikissa koemuodoissa luodaan hallittu ”muuutos”. Tähän viitataan myös Demingin laatuympyrässä PDSA.  SS:ssä kokeen käyttö on havainnointitutkimuksiin alisteista. Erityisesti Shainin systeemi välttää seulontakokeita (screening experiments) hallitsevan syyn etsimiseksi, jotka taasen ovat keskeisiä niin Taguchi kuin Six Sigmassa (L12 ja L18 ortogonaalimatriisit). 

Parannusmatkan (Remedial Journey) kokeet voisivat olla parempia SS:ssä. Vaihtelun pienentämiseksi prosessin asetuksissa, ohjaussuunnitelmassa tai tuotteen tai prosessin suunnittelussa on tehtävä muutos; eli muutos yhteen tai useampaan prosessi-inputtiin, joka on kiinteä normaalissa tuotannossa. Näitä muutoksia voidaan etsiä ja tutkia vain kokeiden avulla. Tähän SS ei ota kantaa kun taas Six Sigmassa parannus voidaan optimoida ja simuloida kokeella.

Mittausjärjestelmän tärkeyden painottaminen on SS-algoritmin vahva kohta kuten myös Six Sigmassa. Six Sigmassa käytetään numeerista Gage R&R ja <10 % sääntöä joka vastaa Shainin sääntöä ∆P/∆M>6. 

DMAIC sopii hyvin Shainin systeemiin tai päinvastoin. D, M ja A vastaavat diagnostiikkamatkaa ja I ja C vastaavat parannusmatkaa. Six Sigman verrattuna SS:n yksittäisten vaiheiden tarkoitus ja strategiat ovat tarkempia ja tarkemmin määritettyjä kuten tekstistä ilmenee.

SS algoritmi on erityisesti suunniteltu keskisuurten ja suurten volyymien valmistusprosessiin, jossa inputit ja outputit voidaan mitata helposti. Tosin Richard Shainin on todennut, että Shainin soveltuu hyvin moniin erilaisiin prosesseihin pienistä suuriin⁽¹¹⁾. Six Sigmalla on kuitenkin paljon laajempi käyttöalueeltaan ja ei vaadi niin suurta prosessituntemusta, mutta vie pidemmän aikaa ja vaatii suurempia kokeita.

Kun noudatetaan Shainin periaatteita, siinä käytetään sarjaa iteratiivisia askeleita, joilla lähestytään punaisen X:n tunnistamista. Seuraavat vaiheet löytyvät jokaisesta onnistuneesta SS-projektista:

1. Rajaa projektin painopiste yhteen ongelmaan.
2. Kehitä vihjeiden luomisstrategia, joka pohjautuu ongelman, järjestelmän tai prosessin luonteen. Alussa strategia ei koskaan sisällä muuttujien luetteloa esimerkiksi Ishikava-diagrammia ja sen luomaa ”idea”luetteloa.
3. Toteuta strategia, jolla eliminoidaan laajat mahdolliset vaihtelulähteet. Vihjegeneraattorit ovat tilastollisia työkaluja, jotka hyödyntävät kerrostumista (stratification) ja erittelyä (disagrigation), jotta voidaan löytää suurimmat vaihtelun lähteet. Ne ovat käytännönläheisempiä kuin havaintotutkimukset, mutta vähemmän yksityiskohtaisia kuin suunnitellut kokeet.
4. Päivitä strategia jäljellä olevien mahdollisten vaihtelulähteiden perusteella.
5. Toteuta tarkistetut strategiat ja rajaa hakua entisestään. Se, millainen ongelma on luonteeltaan, vaiheet 4 ja 5 voidaan toistaa useita kertoja.
6. Vahvista Punaisen X:n (Red X) tunnistaminen suunnitellulla kokeella (DOE). Vaiheet 1–5 vastaavat poliisitutkintaa, jonka tuloksena yksi tai useampi epäilty pidätetään. Vaihe 6 vastaa tapauksen viemistä oikeuteen. Tilastoinsinööri (statistical engineering) odottaa saavansa ongelman päälle ja pois päältä kuin valot valokytkimellä ohjaamalla Punaisen X:n syöttötasoja. Vaiheessa 6 jäljellä olevien epäiltyjen määrän perusteella testi voi olla tekijäkoe (factorial experiment) tai yksitekijäkoe (OFAT experiment). Artikkeli: Muutanko yhtä tekijää vai useita tekijöitä? OFAT vai DoE?
7. Ymmärrä Punaisen X ja Vihreän Y:n välinen suhde. Jos Punainen X on itsenäinen päävaikutus, otetaan sopiva näyte suhteen vahvuuden päättelemiseksi suhteessa kaikkiin muihin vaihtelulähteisiin. Jos Punainen X on keskinäisvaikutus, tämä vaihe sisältää vasteen vastepinnan (RSM) optimointimahdollisuuksien tunnistamisen.
8. Harkitse mahdollisia potentiaalisia ratkaisuja. Kun Punaisen X-suhde on ymmärretty hyvin, tämä on sopiva askel mahdollisten parantavien toimenpiteiden aivoriiheksi, mukaan lukien tietojen ja kokemuksen hakeminen operaattoreilta, joiden on toteutettava ratkaisu. Jos Punainen X on pääefekti, mahdollisuudet hallita sillä koko satunnaista vaihtelua ovat rajalliset; sitä on yksinkertaisesti valvottava tiukemmin. Toisaalta, kun Punainen X on keskinäisvaikutus, optimoinnille on usein useita vaihtoehtoja.
9. Toteuta parantavat toimet ja seuraa tuloksia. Tämä on sopiva vaihe PDSA:lle sen varmistamiseksi, että parantavat toimet tuottavat odotetut tulokset eivätkä aiheuta tahattomia ongelmia ja sivuvaikutuksia.
10. Hyödynnä saatuja kokemuksia. Useimmissa tapauksissa Punainen X on yllätys, joka johtaa syvempään ymmärrykseen joko tuotteesta tai prosessista. Tätä syvällistä tieto tohtori Deming tuki ja kehotti hankkimaan. Saadut oivallukset tulee välittää insinöörille tuotteen tai prosessin suorituskyvyn matemaattisten mallien parantamiseksi ja tulevaisuuden suunnittelun parantamiseksi.

7. Shainin systeemin keskeiset työkalut

Shainin systeemissä on lukuisia ainutkertaisia työkaluja, joista kymmenkunta muodostaa keskeisen osan systeemiä.

7.1. Luo tehokas mittaussysteemi:

Visuaalisen mittausasteikon muunnos (Visual Scoring Transform) muodostaa viivaimen, joka muuntaa attribuuttidatan (yhdenmukainen, ei- yhdenmukainen) muuttujadataksi. Tämä uusi asteikko antaa mahdollisuuden nähdä vaihtelun yhdenmukainen (conformance) ja ei-yhdenmukainen (non-conformance) osien sisällä. Sovelletaan tarvittaessa.

Vastusrajan muunnossta (Resistance Limit Transform) käytetään, kun tutkittava laatuominaisuus on vastusraja, jonka attribuutintulos on rikki tai rikkoutumaton (esim. valukappaleen lujuus, jonka on kestettävä 50 yksikköä kineettistä energiaa). Sovelletaan tarvittaessa. 

Isoplot (Isoplot) on graafinen tekniikka, joka erottaa tuotevaihtelun ja mittausvirheen ja antaa kullekin arviot, jotta mittausjärjestelmän erottelukyky voidaan tunnistaa. Yksinkertaisimmassa muodossaan valitaan 30 yksikköä ja jokainen yksikkö mitataan kahdesti ja näistä ”pari”mittauksista laaditaan sirontakaavio. Käyrällä vaaka ja pystysuuntainen vaihtelu on edustaa prosessin kokonaisvaihtelua ∆S ja kohtisuorassa 45 asteen käyrää edustaa mittausvaihtelua ∆M ja ∆P prosessi/tuotevaihtelua. Erottelukyvyksi vaaditaan vähintään ∆P/∆M>6, jotta mittausjärjestelmä on kyvykäs. 

7.2. Vihjeiden generointi

Sen jälkeen kun on määritelty, että mittausjärjestelmä on kyvykäs, voidaan jatkaa vihjeiden luomista (glue generation). Monimuuttujatutkimukset ovat SS ongelman-ratkaisustrategian ydin ja myös vaihe, joka erottaa sen muista lähestymistavoista. Useimmat tekniset ongelmastrategiat perustuvat arvaukseen, jotta voidaan laatia luettelo mahdollisista juurisyistä. Näitä arvauksista voidaan sitten hakea juurisyytä testaamalla ja kokeilla, joilla synnytetään keinotekoinen muutos. Juurisyy on syyn muutos, kausaliteetti, joka muuttaa haluttua ominaisuutta Y ∆Y:n verran. Arvailun sijaan Shainin systeemi luottaa osien kanssa puhumiseen (talking to the parts). Tämä voidaan toteuttaa keräämällä uutta empiiristä dataa prosessin ulostuloista (output) suunnitellun tiedonkeruun avulla. 

Kuten ongelmanratkaisustrategioita käsittelevässä osiossa mainittiin, aloitamme laajoilla kysymyksillä ja laajoilla multivareilla. Näin voimme eliminoida suuren määrän epäiltyjä muuttujia muutamalla kysymyksellä. 

Multi-Vari-kaaviot palvelevat tätä tarkoitusta hyvin. Multi-Varissa osat kerätään peräkkäin tuotannosta eikä satunnaisesti. Jokaisesta näytteestä otetaan vähintään kolme peräkkäistä osaa. Näytteitä otetaan eri aikoina työvuoron aikana. 

Vaikka monimuuttujakaavio (Multi-Vari) on hyödyllinen lähtökohta epäiltyjen muuttujien määrän vähentämiselle, saatetaan joutua käyttämään ylimääräisiä vihjegeneraattoreita epäilyttävien muuttujien luettelon vähentämiseksi entisestään. 

Pitoisuuskaaviot (Concentration Diagrams ) näyttävät kappaleen sisäistä vaihtelua yksityiskohtaisemmin kuin Multi-Vari-kaavio. Vikojen sijainnin merkitsemiseen käytetään osakaavioita.

Parittainen vertailut (Paired Comparisons) ovat sopivia, kun suurin vaihteluperhe on osasta osaan. Analyysiin valitaan kahdeksan paria osia, joista jokainen sisältää hyvän osan ja huonon osan. Jokaisen parin muodostavat osat pitäisi ottaa tuotantoprosessista niin läheltä toisia kuin mahdollista. 

Komponenttihakukuviot (Component Search Patern, Component swap) ovat tehokkaita, kun laatuominaisuus, johon yritämme vaikuttaa, on kokoonpanon (esim. pumpun, mittarin tai piirilevyn) tulos yksittäisen osan ominaisuuden sijaan. Jos löydämme kaksi kokoonpanoa, joilla on merkittävästi erilaiset lähtötasot, voimme löytää eron syyn käyttämällä komponenttihakukuvioita.

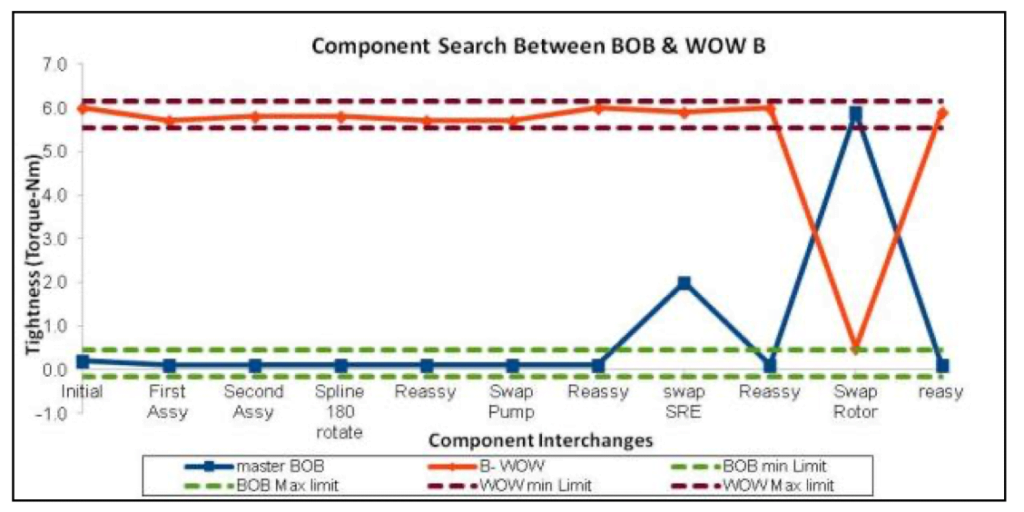
Riippumatta siitä, mitkä vihjeiden generaattorit ovat sopivia, voidaan siirtyä seuraavaan vaiheeseen, kun on vähennetty epäiltyjen määrää hallittavissa olevaan määrään. Vihjeiden luominen toimii, koska vaihtelulla on aina yksi suuri syy, Punainen X, ja tämä syy erottuu muiden joukosta neliöaksiooman summan neliöjuuren ansiosta. 

7.3. Punaisen X:n eristäminen

Tilastollisesti suunniteltuja kokeita (Statistically Designed Experiments, SDE tai DOE) käytetään punaisen X:n tunnistamiseen ja sen vaikutuksen suuruuden arvioimiseen prosessin nykyisellä toiminta-alueella. 

Punainen X on usein kahden tai useamman riippumattoman muuttujan keskinäisvaikutus. Nämä keskinäisvaikutukset ovat lähes aina yllätys, kun ne havaitaan SDE (DOE):n avulla. Tämä kuvaa juurisyyn löytämisen vaikeutta. Paraskaan asiantuntija ei tiedä ja osaa arvata juurisyytä! Koska näitä vaikutuksia ei voida ennustaa ja koska ainoa tapa tunnistaa ne, on tilastollisesti suunniteltu koe, SS:ssä vältetään käyttämästä osittaistekijäkokeita (fractional factorials experiments). 

Huom! Screening-koetta koskeva argumentti ei enää ole täysin pitävä. Vuonna 2011 Tri Bradley Jones ja prof Chris Nachtsheim keksivät DSD-kokeet Definitive Screening Designs, jotka mahdollistavat keskinäisvaikutusten tutkimisen screningkokeilla. Aihetta käsitellään QKK:n Black Belt -kurssilla ja artikkelissa Onko DSD-koesuunnitelmat vuosisadan merkittävin parannus- ja koesuunnitteluinnovaatio?.

Muuttujahakumallia (Variable Search Patterns) käytetään, kun epäilyttäviä muuttujia on viisi tai enemmän. Nämä noudattavat samoja sääntöjä kuin komponenttihaku-mallit (Component Search Patterns); kuitenkin jokaisen epäiltävän muuttujan kahta tasoa, tyypillisesti korkeaa ja matalaa, käytetään hyvien ja huonojen komponentti-parien sijasta.

B vastaan C (B vs C ):ää käytetään punaisen X:n vahvistamiseen, jos jäljelle jää vain yksi epäilty muuttuja vihjeiden luomisen jälkeen. Tämä on yksisuuntainen arvo-järjestyksen hypoteesitesti, joka vahvistaa, että uusi taso B (parempi) tuottaa parempia tuloksia kuin nykyinen taso C.

Satunnaistaminen on välttämätöntä SDE:n suorittamisessa. Jos Punainen X on jätetty pois kokeesta, satunnaistaminen varmistaa, että mahdollisuus päästä väärään johtopäätökseen rajoittuu kokeeseen suunniteltuun alfariskiin. Satunnaistamisen epäonnistuminen mitätöi kokeen tilastollisen validiteetin.

7.4. Realististen toleranssien määrittäminen

Toleransseja ei pidä asettaa mielivaltaisesti. Menettely rationaalisten toleranssien määrittämiseksi seuraa loogisesti tilastotekniikasta (statistical engineering).

Toleranssisuunnikas (Tolerance ParaIlelogram) liittäminen sirontadiagrammiin luo tilastolliset rajat Punaiselle X:lle, mikä varmistaa asiakkaiden kiinnostuksen. Nämä rajat ovat realistinen toleranssi.

7.5. Tilastollisen prosessin ohjauksen toteuttaminen

Esiohjausta/valvontaa (precontrol) käytetään Shainin Systemissä prosessiohjaukseen. Sen tarkoituksena on tarjota prosessin aktiivista ohjausta valvonnan sijaan. Se on työkalu, jonka avulla käyttäjä määrittää, milloin prosessin on annettava käydä ja milloin on tehtävä säätö.

8. Shainin ja Six Sigma -menetelmät ja niiden yhtenevyydet ja erot 

Kuten aikaisemmin on mainittu, Dorian Shainin oli luomassa keskeisiltä osaltaan Six Sigmaa. Ei ole ihme, että osa työkaluista ovat tuttuja Six Sigmasta, jonka jo aika moni Suomessa tunteekin. Myös Taguchi-menetelmään on suorat yhteydet. Vaikuttaa, että osa Shainin työkaluista ja ideoista on tuotu Taguchilta ja edelleen Six Sigmaan. 1980-luvulla laatukentässä vallitsi kiivas keskustelu osittaistekijäkokeiden, screening-kokeiden ja toisaalta täystekijäkokeiden asemasta ja parametrisuunnittelun menetelmistä. Jälki näkyy Shainin Systeemissä. Shainin pitäytyi täystekijäkokeissa ja korostaa keskinäisvaikutusten tärkeyttä ja Six Sigmassa käytetään ensi sijassa osittaistekijäkokeita ja parametrien epälineaarisuutta vastepintakokeiden (RSM) yhteydessä ja optimoitaessa. 

Keskeiset erot Shaininin ja Six Sigman välillä ovat tilastollisen analyysin roolissa sekä projektin suunnittelussa ja toteutuksessa. Six Sigmassa käytetään perinteisiä tilastollisen analyysin työkaluja kuten GLM:ää, varianssianalyysiä (ANOVA) regressioanalyysiä, suunniteltuja kokeita, hypoteesitestejä ja ohjauskaavioita. Nämä vaativat käytännössä ohjelman kuten Minitab. Six Sigmassa projektit alkavat yleensä aiheen asiantuntijoiden kokouksella, jossa laaditaan luettelo mahdollisista syistä aivoriihen ja kalanruotokaavion johdattamana. Projektin onnistuminen riippuu siitä, onko todellinen juurisyy listalla. Siksi Six Sigma tiimit valitsevat enemmän mahdollisia syitä kuin vähemmän. Tämä on laajentava lähestymistapa, joka usein synnyttää useita rinnakkaisia aktiviteetteja. Tilastollinen tutkiva analyysi (EDA) suosii suuria tietojoukkoja, joista lasketaan vihjearviointeja esim. GLM:llä tai Big-datalla. Tämä tekee tilasto-ohjelmistojen soveltamisesta välttämätöntä. Kuitenkin hyvin harvoin, jos koskaan suurista datamääristä löydetään juurisyytä, vihjeitä kyllä. Katso artikkeli: Edam ja EDA?

Tilastollisen ongelmanratkaisun alleviivaava periaate on Y = f(x). Tämä saa tiimit tunnistamaan kaikki tekijät, jotka voivat mahdollisesti vaikuttaa avainulostulon (Y) arvoon. Tämän yhtälön laajennus on Y = a + bx₁ + cx₂ + dx₃ + … + mx_n. Onnistunut projekti löytää kaikki kertoimet (a, b, c, d jne.), jotka ovat tilastollisesti merkitseviä. DMAIC (Define, Measure, Analyze, Improve and Control) -prosessi yhdessä Minitab ohjelman kanssa tukee tätä lähestymistapaa, jossa luodaan matemaattinen malli.

Shainin -hankkeet ovat näyttöön perustuvia; lähestyen suurinta vaihtelulähdettä, Punaista X: ää. Shainin -projekti alleviivaava periaate on ∆y = f (∆x). Tämän yhtälön laajennus on ∆y = a + b∆x1 + c∆x2 + d∆x3 + … + m∆xn. 

Keskittymällä vaihteluun, ts. Y: n muutokseen ∆Y, tavoitteesta tulee suurimman termin löytämistä, kun taas Six Sigmassa haetaan mallia. Suurin arvo muodostuu merkittävän kertoimen yhdistelmästä ja suuresta muutoksesta X: ssä. Tämä termi on harvoin termi, jossa on suurin kerroin. Pareto -periaate vaatii huomattavan eron näiden kertoimien ja muutoksen osuudessa, joka vaikuttaa Y: n. 

Shainin -tutkinnan tavoitteena on lähentyä nopeasti muutamia kriittisiä termejä, jotka muodostavat suurimman osan vaihtelusta. Monissa projekteissa Punainen X on keskinäisvaikutus riippumattomien inputtien (X) välillä. Tätä ei voi millään asiantuntia ”ulkopuolelta” havaita tai tietää.  Shainin -työkalut ovat erittäin tehokkaita paljastamaan nämä keskinäisvaikutukset. Six Sigmassa tyydytään päätekijöiden päävaikutuksiin (juurisyihin) Taguchin tapaan. Taguchi varoittaa keskinäis-vaikutuksista ja sanoo, että niitä ei saa käyttää ”epävakauden” vuoksi. Shainin taas käyttää nimenomaan keskinäisvaikutusta – Japanilainen ja länsimainen ratkaisu.

Shainin -projektit sisältävät kriittisten suhteiden löytämisen tiukan etsivätyön avulla. ”Dick” Shainin kuvaa Shainin tekniikkaa Sherlock Holmsin ja Watsonin välillä:  

” Jos kuvailet ihmisille tapahtumasarjaa, useimmat heistä kertovat sinulle, mikä olisi lopputulos. He voivat koota nämä tapahtumat mielessään ja väittää niiden perusteella, että jotain tapahtuu. On kuitenkin vain vähän ihmisiä, jotka, jos kertoisit heille lopputuloksen, pystyisivät kehittämään omasta sisäisestä tietoisuudestaan, mitkä olivat ne askeleet, jotka johtivat siihen tulokseen. Tätä voimaa tarkoitan, kun puhun taaksepäin päättelystä tai analyyttisestä päättelystä… On viisikymmentä henkilöä, jotka voivat järkeillä synteettisesti ja yksi henkilö, joka osaa ajatella analyyttisesti.” 

RCA ja Shainin, Six Sigma ja Taguchi ovat taaksepäin ajattelua. Shainin puhuu osien kanssa ja löytää Punaisen X: n hyödyntämällä suorituskykyeroja parhaiden ja huonoimpien osien välillä. Sen sijaan, että pyydetään asiantuntijoita luetteloimaan mahdolliset syyt, Shainin käyttää heidän oivalluksiaan kehittääkseen strategian osien pakottamiseksi paljastamaan niiden välillä olevat erot. Shainin -ongelmanratkaisu etenemissuunnitelma on FACTUAL (tarkenna, lähestymistapa, lähentyä, testaa, ymmärrä, sovella, levitä).

Lähestymistapa on yksi keskeisistä eroista FACTUALin ja DMAIC:n välillä. 

1) Lähestymistavan aikana insinööri kehittää hakustrategian, joka perustuu ongelman luonteeseen ja BOB- ja WOW-osien saatavuuteen. Tämän strategian toteuttaminen mahdollistaa sen, että insinööri voi nopeasti lähentyä keskeisiä inputteja eliminointiprosessin kautta. Vaikka Shainin-tekniikat ovat tilastollisesti tarkkoja, graafinen analyysi pitää tilastot taustalla ja rohkaisee teknisiä näkemyksiä kriittisiin suhteisiin. Shaininin painotus oivaltavaan graafiseen analyysiin syrjäyttää useimmat tilastolliset laskelmat. Shainin-työkalut ovat riittävän yksinkertaisia, jotta ei tilastotekniikkaa tuntevat voivat käyttää niitä oikein, mutta silti riittävän kehittyneitä ratkaisemaan erittäin monimutkaisia ongelmia, jotka liittyvät valmistuksen laatuun, tuotteen suorituskykyyn ja luotettavuuteen.  

2) FACTUALin testivaihe on toinen keskeinen ero DMAIC:iin. Testivaiheen aikana ryhmien on osoitettava ymmärtävänsä juurisyy kytkemällä ongelma päälle ja pois. Tätä vaihetta voi kuvata Punaisen X:n viemisenä oikeuteen. Lähestymis- ja lähenemisvaiheet edustavat etsivätyötä, testivaihe edustavat syyllisyyden osoittamista ilman epäilystäkään. Testivaihe suojelee yrityksiä investoinneilta, jotka voisivat kohdistua ratkaisuihin, joissa on väärän juurisyy. Niissä tapauksissa, joissa testi ei vahvista punaista X:ää, tiimi palaa lähestymis- ja supistamisvaiheisiin löytääkseen puuttuvat vaikuttajat.

3) Y -> X:n konvergenttia noudattamalla Shainin löytää Red X:n nopeasti ja tehokkaasti. Hyödyntämällä eroja Shainin minimoi ajan, osien määrän, ihmisten ja arvokkaiden resurssien, joita tarvitaan todellisen juurisyyn löytämiseen. Shainin-tutkimuksilla on rikas historia ratkaisemattomiksi pidettyjen ongelmien ratkaisemisessa, sillä ne ovat löytäneet yllättäviä suhteita, joita ei koskaan tullut esille aiheen asiantuntijoiden kanssa käydyissä aivoriihitapaamisissa.

Shainin-tekniikkaa suosivat usein insinöörit ja asiantutijat, jotka ymmärtävät asioiden toimivuuden ja arvostavat odottamattomien suhteiden löytämistä. DMAIC-tekniikoita suosivat matemaatikot ja vähemmin asiaa tuntevat, jotka osaavat enemmän laskelmia ja analyysejä ja jotka etsivät täydellisiä malleja syy-seuraussuhteista. Yhdistettynä erinomainen combo!

9. Yhteenveto ja johtopäätökset

Juurisyyn eli vaikuttavan hallitsevan syyn, kausaliteetin, hakemisen ja löytämisen suurin este on tyytyminen pinnalliseen analyysiin, josta kirjoitin artikkelin⁽³⁾. Väitetään, että vain joka kymmenes ongelmia ratkaiseva henkilö tuntee ja osaa juurisyyanalyysimenetelmän ja ymmärtää, että vain juurisyyhyn tehty muutos korjaa ja parantaa systeemiä. 

Mikä johtaa pinnalliseen analyysiin? Uskoakseni siihen on syynä lukuisat arkielämän virheelliset käsitykset: uskotaan, että syy tiedetään kokemuksesta; minä kyllä tiedän, olen asiantuntija; mitä sitä tutkia, kaikki vaikuttavat kaikkeen tasapuolisesti, aina on lukuisia syitä asiasta riippumatta; juurisyyn löytää helposti talonpoikaisjärjellä, haluamme vain uskoa omaan mielipiteeseemme, ei tunneta juurisyyn teoriaa ja menettelyjä. Tässä muutamia luuloja ja uskomuksia tiellä kohti pinnallista ja virheellistä syytä ja vääriä toimenpiteitä … ja lisääntyviä kustannuksia.

Tosiasia on, että juurisyyn, toiselta nimeltä kausaliteetin, hakeminen on vaativa tehtävä, jossa tarvitaan erityisiä hakualgoritmeja ja ehdottomasti testi, koe (DOE) asian varmistamiseksi. Lähes poikkeuksetta juurisyy on yllätys hakijalleen … ja huudahdus tämä ei voi olla totta!

Aina nämä algoritmit eivät kuitenkaan ole tilastollisesti vaativia. Tarvitaan vain oikea olosuhde ja kysymyspatteri ja järjestys, jolla haku onnistuu. Tästä esimerkkinä Logiikkapuu (RCA1), Tap Root, 7 Tools, LPM, A3, D8, Kaizen jne. Nämä kaikki työkalut toimivat olosuhteessa, kun tuotteessa, prosessissa, systeemissä on tapahtunut voimakas muutos. Tämä muutostekijä tunnistetaan ja tehdään korjaava toimenpide. Kansankielellä prosessi, tuote, palvelu on rikkoutunut ja halutaan löytää juurisyy tällä rikkoutumiselle ja korjaus. Tätä korjausta usein kutsutaan virheellisesti ”parannukseksi”.

Vaativimmasta päästä on sitten Lean Six Sigma, Shainin ja Juran Breaktrough ja ehkä Taguchi, joilla voidaan murtaa stabiili prosessi tai systeemi ja löytää juurisyy. Tämän algoritmin ydin on koe (DoE). Tämä mahdollistaa aidon suorituskyvyn parannuksen, jolla on liiketoiminnallista ja taloudellista vaikutusta. 

Välialueen harmaa vyöhyke on puolistabiili tilanne, jossa prosessissa on pienehköjä muutoksia, joiden avulla voi yrittää haravoida herkillä tilastollisilla ja kokeellisilla menetelmillä juurisyitä esimerkiksi RCA 2, RCCA, Apollo, Kepner Tregoe, EPS, jne. ja saada jopa parannusta aikaan.

Mistä olisi hyvä lähteä liikkeelle, jos haluaa oppia RCA-menetelmät tai ainakin keskeiset osat niistä ja niiden periaatteista? Itse lähtisin liikkeelle vaativammasta päästä, Lean Six Sigma ja laajentaisin Shainin Systeemiin. Oma reittini kulki Juran -> Taguchi -> Shainin -> Six Sigma. (Juranin Breakthrough 1983 Helsinki, Taguchi 1987 Tukholma, Shainin 1990 USA, Six Sigma USA 1997). Kun näiden menetelmien sanoman ja menettelyn oivaltaa ja osaa, muut RCA-menetelmät ovatkin sitten helppoa ”kauraa”. 

En voi laadussa keksiä tärkeämpää kuin ongelman ratkaisumenetelmät, juurisyyanalyysi, ja näiden opettaminen ja soveltaminen organisaatiolle. Laatupalkinnot ja järjestelmät ovat toissijaisia, mutta kylläkin tärkeitä. Ajatellaan lääkäriä. Hän osaa syöttää potilastietoja järjestelmään, mutta ei osaa diagnosoida sairautta. Minä valitsen lääkärin, joka osaa diagnostisoida!

10. Shainin Systeemin käyttöesimerkkejä

Tutkijat Priyesh Sanghvi, Naitik Devgania, Girish Deshpande, Nitin M Pathak esittävät artikkeliyhteenvedossa REVIEW OF LITERATURE ON SHAININ METHODOLOGY 2017 yhteenvedon Shainin Systeemistä ja lukuisia käyttöesimerkkejä Shainin menetelmästä(²⁴⁾.

11. Viitteet

1. Artikkeli: Juurisyyanalyysi ja sen kehittyminen (5.1.2023)
2. Artikkeli: Juurisyyn löytämisen strategioita (23.1.2023)
3. Artikkeli: Juurisyyanalyysi vai pinnallinen syyanalyysi? (16.2.2023)
4. Artikkeli: Pimeän näytön juurisyyanalyysi (RCA) (9.3.2023)
5. Juran, J. M. (1988). Juran’s Quality Control Handbook, 4th ed. New York: McGraw-Hill.
6. Hoerl, R. W., Snee, R. D. (2003). Statistical Thinking, Improving Business Performance. Pacific Grove, CA: Duxbury.
7. https://asq.org/about-asq/honorary-members/shainin
8. https://en.wikipedia.org/wiki/Dorian_Shainin
9. Jan Kosina: Quality improvement methods for identification and solving of large and complex problems; Journal of Interdisipline Rearch, 2015
10. https://cp.shainin.com/wp-content/uploads/2018/04/Shainin-vs-Six-Sigma.pdf
11. Richard D. Shainin: Statistical Engineering: Six Decades of Improved Process and Systems Performance, Quality Engineering, vol 24, 2012
12. Stefan H. Steiner , R. Jock MacKay & John S. Ramberg: An Overview of the Shainin SystemTM for Quality Improvement, Quality Engineering, vol 20, 2008
13. Juran, J. M , Gryna, F. M. (1980). Quality Planning and Analysis, 2nd ed. New York: McGraw-Hill.
14. Shainin, R. D. (1995). A common sense approach to quality management. 49th Annual Quality Congress Proceedings, ASQC, pp. 1163- 1169.
15. Shainin, R. D. (1993). Strategies for technical Problem solving. Quality Engineering, 5:433-438.
16. Shainin, P D., Shainin, R. D., Nelson, M. T. (1997). Managing statistical engineering. 51st Annual Qualit y Co ngress Proceedings, ASQC, pp. 818-532.
17. Shainin, P. D. (1993) Managing quality improvement. 47th AnnualQuality Congress Proceedings, ASQC, pp. 554- 560.
18. Shainin, P. D. (1992). Managing SPC, a critical quality system element, 46th Annual Quality Congress Proceedings, ASQC, pp. 251–257.
19. Joiner, B. J. (1994). Fourth Generation Management: The New Business Consciousness, McGraw-Hill, New York.
20. Bhote, K. R., Bhote, A. K. (2000). World Class Quality, 2nd ed. NY: American Management Association.
21. Seder, L. A. (1990). Diagnosis with diagrams. Quality Engineering, 2:505–530 (reprinted from original in Industrial Quality Control, 1950).
22. B. Shanmugam, Dr. K. Kalaichelvan, Rejection reduction of Vacuum Pump type Alternator Assembly, IOSR Journal of Mechanical and Civil Engineering, 2014
23. Nagaraja Reddy K M, Dr. Y S Varadarajan, Raghuveer Prasad, Quality Improvement during Camshaft Keyway Tightening Using Shainin Approach, International Journal of Scientific and Research Publications, Volume 4, Issue 7, July 2014
24. http://www.ijarse.com/images/fullpdf/1515839586_ME001.pdf
25. D. Shainin: The Shainin approach (Seminar 1990, USA)
26. Stefan H Steiner, R. Jock Mackay, Statistical Engineering – An Algorithm for Reducing Variation in Manufacturing Processes, 2005