Laadun perustyökalut – Pareto, histogrammi ja ohjauskortti?

Pareto, histogrammi ja ohjauskortti muodostavat osan peruslaatutyökaluista, joista yleensä käynnistyy ongelmanratkaisu niin erityis- kuin satunnaissyidenkin osalta. Seuraavassa tutustutaan näihin työkaluihin ja niiden perusteisiin (luonnon lait).

Pareto-periaate tai 20/80 sääntö

Pareto-diagrammin synnystä on mielenkiintoinen tarina. Sana Pareto tulee italialaisesta taloustutkijasta Vilfredo Paretosta. Pareto tutki Genovassa syvällisesti hyvinvoinnin jakautumista. Hän mallinsi hyvinvoinnin jakautumisen ja havaitsi, että hyvinvointi jakautuu erittäin epätasaisesti. Tätä epätasaisuutta kuvaa Pareto-diagrammi

1940-luvulla laadun guru, J.M. Juran toi termin laatutekniikkaan kuuluisassa kirjassaan Quality Control Handbook ja esitti, että muutamat tekijät (20 %) hallitsevat suurta määrää tekijöitä – ”the vital few and the trivial many”. Samalla Juran yleisti periaatteen ja loi säännön. Niinpä esimerkiksi vain muutama reklamaatiosyy aiheuttaa suuren määrän reklamaatioita. Kysymys on tärkeästä priorisointisäännöstä. Korostan sanaa sääntö! Kaikki tekijät eivät vaikuta kaikkeen, vaikka näin kuulee usein sanottavan.

Pareto-periaatetta (sääntöä) on usein tulkittu väärin. Alapuolella olevissa kuvissa oikea Pareto, jossa 1 (2) tekijää muodostaa/selittää 80 % virheistä. Oikeanpuoleisessa virheellisessä kuvassa neljä tekijää kahdeksasta muodostaa 80 % virheistä. Selvästi kysymyksessä on virheiden syyluokittelun virhe eli mittausvirhe. Tarkastajat luokittelevat tai kirjaavat asiat väärin!

Jos muodostetaan virheiden määrät satunnaisgeneraattorilla, saadaan hyvin paljon virheellistä Paretoa muistuttava kuva. Kuvat tehty Minitab 15 -ohjelmalla. Kokeilepa, millaisia virhe-paretoja saat satunnaisgeneraattorilla. Paretoa käytettäessä on aina tarkistettava, että se on ”oikea” Pareto eikä mittaus- tai luokitteluvirheiden sotkema virhe Pareto. Aivan samanlainen virhe-pareto on tilanteessa, jossa yksi luokka on ylivoimaisen suuri. Mittauksen oikeellisuus on äärimmäisen tärkeää. Tarkastukset, luokittelut, mittaukset on ”kaketettava” eli määritettävä niiden virhe. Tästä myöhemmissä artikkeleissa.

Histogrammi

Histogrammi on toinen tärkeistä laatumenetelmistä. Jos Pareto muodostaa luokitellun datan (esim. virhe tai reklamaatioluokkien) analyysin, histogrammissa muutetaan jatkuva muuttuja (pituus, aika, paino) luokkamuuttujiksi.

Histogrammin tausta on paljon vakavampi kuin usein tullaan ajatelleeksi. Se kuvaa vaihtelua ja sen olemassa oloa, jota ihmiset eivät vieläkään usko tai eivät ymmärrä. Ilmasto lämpenee tai kylmenee, yhtä kaikki. Pitääkö meidän tästä huolestua! Muutos on luonnollinen, muuttumattomuus epäluonnollinen. Juuri näin päin.

Tämä tarina, kuten niin monen muunkin kehityksen tarina, lähtee tähtitieteestä ja tähtien sijainnista. Tähtitieteilijä ja matemaatikko Pierre-Simon Laplace selitti 1809, miksi tähtien paikat vaihtelevat ja esitti virheteorian. Jos 200 vuotta sitten vain tähtien paikat vaihteli, niin tänään sanomme, että kaikkien prosessien ulostulot vaihtelevat. Siis kaikki vaihtelevat! Ja vaihtelun tutkiminen on laatutekniikan ydin. Siihen perustuu innovaatiot ja parannukset kuin virheet ja katastrofit.

Kuinka kuvaamme vaihtelua? Mittaustulokset luokitellaan 8-12 tasaväliseen luokaan ja lasketaan kuinka monta arvoa kuhunkin luokkaan osuu. Mittaustuloksia olisi hyvä olla yli 50. Tämän jälkeen laaditaan pylväspiirros.

Oikean luokittelun, pylväspiirroksen ja myös piirroksesta vedettävien johtopäätösten tekemisessä auttaa suuresti sopiva ohjelma kuten Excel tai Minitab. Käsin tehty histogrammi ei ole enää nykyaikaa. Liian työläs.

Kuvassa eräs data, josta on Minitabilla piirretty kuva (graafinen yhteeenveto) ja sen vieressä vielä datan numeeriset yhteenvedot. Kaunis kuva, mutta mikä on sen sisältö. Mitä pitäisi kuvasta katsoa? Paljonkin, mutta tässä muutamia:

1. Minkä muotoinen histogrammi on? Taas tärkeä sääntö. Onko kuva normaali eli kellokäyrä (Gaussin käyrä), joksi sitä kutsutaan. Näin pitäisi olla lähes aina. Jos ei ole, alat ihmettelemään, miksi se ei ole. Ei-normaalinen käyrä on harvinainen poikkeus. Huomaa kuitenkin, että ”silmällä” on lähes mahdotonta sanoa, onko data normaalia, etenkään jos dataa on vähän. Siksi ohjelmat testaavat tilastollisesti normaalisuuden. Tässä testaus tapahtuu AD-luvulla ja p-arvolla, joka on 0,326. Johtopäätös on, että emme voi sulkea pois normaalisuuden mahdollisuutta. Suomeksi data on normaalinen.
2. Onko moodeja. Kuvassa on 8, 10 ja 12 kohdalla ”piikki”, mutta koska jakauma on normaalinen, emme niistä nyt välitä. Ovat sattumaa.
3. Missä on keskiarvo? Mean = 10,135 Mikä oli tavoite?
4. Mikä on vaihteluväli, range? Mikä on standardipoikkeama, sigma (StDev)? Pienimmän ja suurimman arvon väli R = 12,5-8,0 = 4,5. Tämä on tärkeä luku laatutekniikassa samoin kuin sigma StDev = 1,002. Mitkä olivat toleranssit?
5. Onko yksittäisiä ”karanneita pisteitä”, outliers? Onko prosessi stabiili? Ei ole karanneita pisteitä.

Usein histogrammi sinänsä ei meitä paljon edesauta, jos meillä ei ole tavoitetta, johon histogrammia sovitetaan. Tämä sovitustyökalu on nimeltään suorituskykytutkimus (capability).

Suorituskyky liittää histogrammin spekseihin ja toleransseihin. Voidaan puhua virheistä. Virhehän on yleensä luonnollisesti syntynyt tapahtuma, jota ihminen ei hyväksy ja jolle ei ole olemassa mitään yhtä syytä. Lisätään edellä olevaan esimerkkiin toleranssit LSL=8 ja USL=12. (LSL= Lower Spesification limit, USL = Upper Spesification Limit)

Nyt näemme kuinka paljon on virheitä tapahtunut (Observed Performance) 4% ja kuinka paljon tulee tapahtumaan sattumalta ilmaan mitään erityistä syytä 4,9%. Minitab mallintaa tulevaisuuden (yhtenäinen käyrä). Vain tulevaisuutta voidaan parantaa. Menneisyys voidaan vain korjata. On aika käynnistää parannusprojekti (Six Sigma projekti) sattuman selvittämiseksi. Muuten sattumaa ei saa hallintaan!

Prosessin käyttäytymiskäyrät eli ohjauskortit (= aikasarja analyysi)

Onko kaikki vaihtelu satunnaista? Ei suinkaan. 2 – 4 % vaihtelusta on jonkin yksittäisen syyn aikaansaannosta eli lääketieteen termein akuutti sairaus (satunnainen syy vaihteluun on krooninen syy). Säännön muuten keksi/todisti tieteellisesti Tsebysev 1860-luvulla. Erityissyitä ei todellakaan voi olla paljon!

Kuinka voimme tietää, milloin on kyseessä erityinen syy ja voidaan ryhtyä toimenpiteisiin eli ohjaamaan työtä tai työprosessia. Ratkaisu on Walter A. Shewhartin kehittämät SPC-periaatteet (SPC = Statistical Process Control eli tilastollinen prosessin ohjaus). SPC on teollisuuden diagnoosi vastaten lääkäreiden tautidiagnoosia. On muuten liki sama asia.

Kuinka diagnisoimme erityissyyt? Prosessin käyttäytymiskortit eli ohjauskortit, jotka Walter A. Shewhart loi, perustuvat niin sanottuun 3 sigma paradigmaan (sääntöön) – satunnainen vaihtelu ulottuu keskiarvosta 3 sigman päähän. Jos vaihtelu on suurempaa, on siihen jokin erityinen syy ja syntyy ”karannut piste”. Matemaattisesti 3-sigma rajat on on monimutkainen laskutoimitus, mutta onneksi tähänkin löytyy vastaus, Excel tai Minitab. Rajat voidaan laskea jo 2-3 pisteestä (luvusta), mutta tarkkenevat, jos lukuja on yli 30. Katsokaamme aikaisempaa esimerkkiä

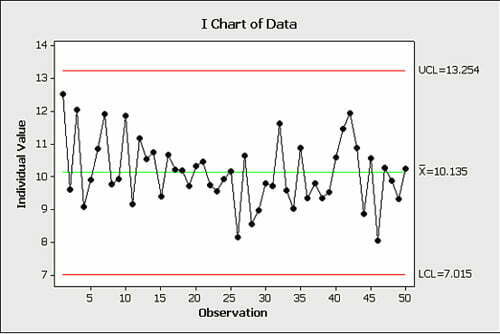
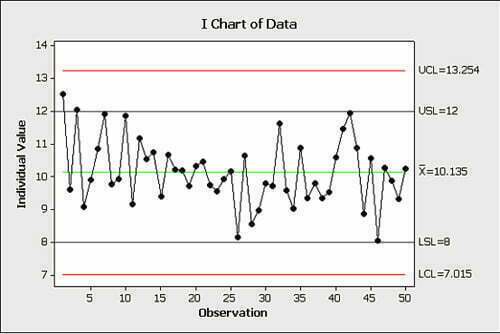
Prosessi vaihtelee satunnaisesti 7,01 ja 13,25 välissä. Näitä punaisia rajoja sanotaan ”luonnollisiksi rajoiksi” (LCL = Lower Control Limit ja UCL = Upper Control Limit) ja rajojen välissä olevaa käyrän vaihtelua luonnolliseksi, jossa yksittäisillä pisteillä, tapahtumilla ei ole yhtä selitystä. Toisin sanoen et voi ohjata prosessia näitä rajoja tiukemmaksi. Voit toki muuttaa prosessin, mutta se vaati Six Sigman. Huomaa, että kuvassa pisteiden 1-25 välillä vaikuttaisi olevan laskevaa suuntausta, mutta tämäkin on sattumaa.

Kun näihin rajoihin liitetään toleranssit LSL= 8 ja USL=12 (katso edellinen esimerkki) havaitsemme että satunnaiset virheet menevät speksirajojen yli mutta luonnollisten rajojen alle.

Prosessin suorituskyky ei täytä vaatimuksia. Valitettavan yleinen tilanne. Yleensä näin käy, jos ammattimies tai nainen säätää prosessin ilman SPC:n ja koesuunnittelun (DoE) työkaluja käyttäen toleranssirajoja. Virheitä (sattumaa) tutkimalla emme voi parantaa laatua, koska virhe on satunnainen. Minimi laatutaso, johon virheitä tutkimalla voi päästä, on 6,6%, mutta normaalisti taso on 10-30% välissä. Muutenhan voisimme oppia lottoamaankin oikein!

On tutkittava prosessia ja muutettava se suorituskykyisemmäksi. Laatutekniikka mahdollistaa virheettömyyden, joka on 1000-10000 kertaa parempi kuin ”ammattimiehen tai naisen taso”. Vertaa ammattimiehen silmät ja mikroskooppiteknologia. Paljonko tarkemmin nähdään mikroskoopilla ”luomu” silmiin nähden? Menestyvät yritykset käyttävät laatutekniikkaa. Paljonko paremmin yrityksesi menestyisi, jos käyttäisi laatuteknologiaa?

Yhteenveto

Olen käsitellyt kolmea erittäin tärkeää periaatetta, luonnon sääntöä.

1. Pareto-periaate. 20-80 sääntö. Yleinen uskomus on, että kaikki vaikuttavat kaikkeen. Uskomus on väärä. Vain muutama tekijä vaikuttaa eli ”the vital few and trivial many”. Keskity vähempään, saat enemmän!
2. Histogrammi, normaalijakaumasääntö. Vaihtelun hyväksyminen kaikkialla on edelleen osalle ihmisiä täysin mahdotonta, vaikka ”keksinnöstä” on jo 200 vuotta. Edelleen haetaan yhtä syytä reklamaatioon ja virheisiin, ei kuten pitäisi ratkaisua vaihteluun. Vaihtelu noudattaa liki aina normaalijakaumaa. Verratkaamme kaikkia ilmiöitä tätä jakaumaa vasten. Kun histogrammiin lisätään vaatimus eli spesifikaatiorajat, saadaan selville ”luonnollisista tapahtumista ne, joita ihminen ei hyväksy”. Näitä sanotaan virheiksi. Virheet voidaan poistaa, kun prosessien suorituskyky parannetaan riittäväksi. Opettele suorituskyvyn parannustekniikka eli Six Sigma.
3. Prosessin käyttäytymiskäyrä eli ohjauskortti ja 3 sigma sääntö. Ohjauskortti perustuu kolmanteen tärkeään laatutekniikan periaatteeseen, 3 sigma paradigmaan. Ilmiöt, tuotteet, tapahtumat, palvelut, mitkä tahansa poikkeavat keskiarvostaan luonnollisesti 3 sigmaa. Rajat ovat joko laajat tai kapeat. Miten milloinkin! Ohjelmalla saat ne laskettua. Jos yrität säätää prosessiasi kohinasta, sinulle käy ”ohrasesti”. Vaihtelu kasvaa ja virheet lisääntyvät. Jos havaitset erityissyyn eli akuutin sairauden, voit syyn löytää ja prosessi stabiloituu tai kansankielellä ”paranee”. Tämä voi myös olla projektin aihe, stabilointi.